Advanced Topics in Network Science
September 11, 2025
Module 02: Small World Networks
Advanced Topics in Network Science
Sadamori Kojaku
skojaku@binghamton.edu
Quiz
Let us denote the adjacency list of a directed graph as follows:
where \(i, j, k, \ldots\) are the nodes in a graph, and there are directed edge from \(i\) to \(j\) and from \(i\) to \(k\).
Identify the number of strongly connected components in the following graph.
What You’ll Learn in this Module
- How to measure distance between two nodes
- Clustering coefficient
- Small-world properties
- A mechanistic model for small-world networks: Watts-Strogatz model
- Libraries for network analysis
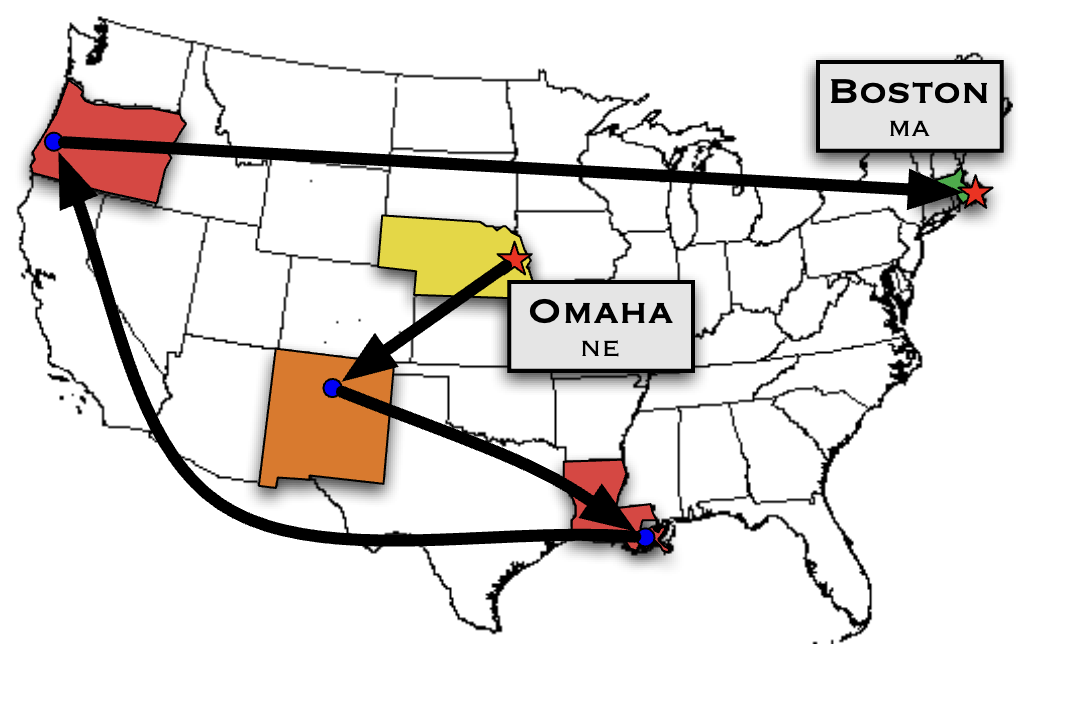
The Small-World Experiment
Stanley Milgram (1933-1984)
- American social psychologist
- Famous for obedience experiments
- Conducted groundbreaking research on social networks
- Revealed surprisingly short chains connecting people


- Recipients in Omaha, Nebraska, and Wichita, Kansas asked to forward a package to a target person in Boston if they knew them
- If not, forward to someone they knew who might know the target
- Chain continued until reaching the target

- Out of 160 letters sent, 64 successfully reached the target
- Average chain length: nearly 6 people
- Later called “six degrees of separation”
Despite hundreds of millions of people in the US, their social network was remarkably compact!

Modern Confirmations:
- Yahoo Research (2009): Email chains, average length ~4-7
- Facebook Study (2012): 721M users, average path length 4.74

Experiencing Small-World: Wikirace
Play the game: WikiRace
- Start from one Wikipedia page
- Navigate to another page using only links
- Experience how few clicks separate any two topics

Question 🤔:
Why are people in the world connected by a small number of steps?
Think about your family tree:
How many ancestors do you have in each generation?
- 1 generation back (parents)
- 5 generations back?
- 10 generations back?
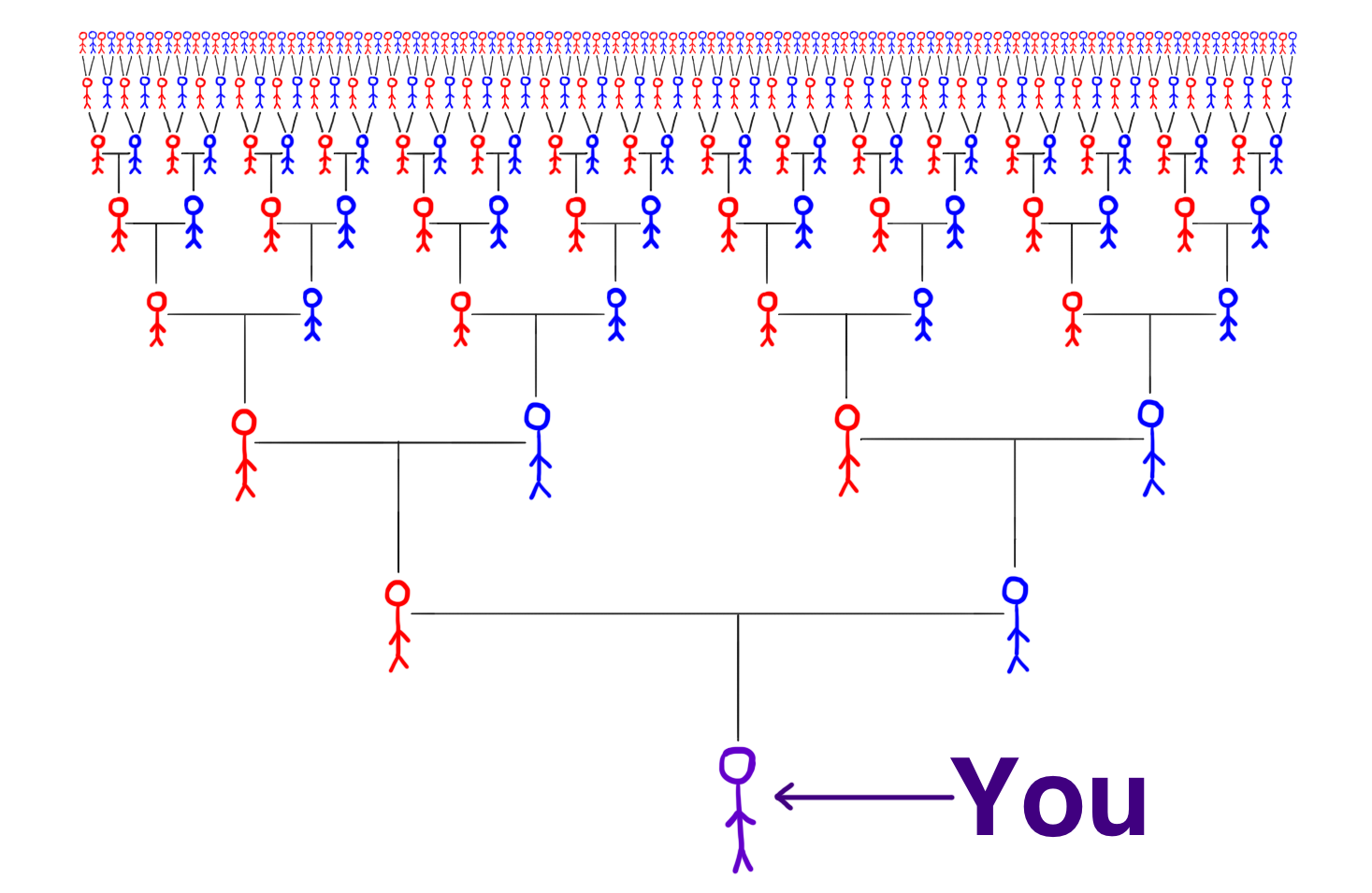
- Ancestors double each generation \(\rightarrow\) exponential growth.
- In social networks, having more than 2 friends means you can reach billions in just a few steps. \(\leftarrow\) does this explain the small-world property 🤔?
Wait, think about 100 generations back
- 100 generation \(\simeq\) 2000 years
- The number of ancestors is \(2^{100} \simeq 10^{30}\)
- But, population in 2000 years ago was only 200 million.
Then, what’s wrong with the estimate 🤔?
- The family tree isn’t a true tree—many ancestors overlap (due to incest).
- Local connections are more common in social networks—your friends are also friends with each other.
- Exponential growth alone doesn’t explain short social distances!

Key question
- If people are connected locally, then our social networks are NOT small-world.
- But observations show that it is small-world.
- So, how can a network have lots of local connections and still remain globally compact 🤔?
- Let’s make it clear what we mean by local and global connections.
Clustering Coefficient (1)
Local clustering asks: given all your friends, how many of triangles you and your friends form, relative to the maximum possible number of triangles?
\[ C_i = \dfrac{\text{\# of triangles involving } i \text{ and its neighbors}}{\text{\# of edges possibly exist in the neighborhood of } i} \]
- Node A has 5 neighbors
- Triangles with A: 2
- Possible triangles: \(\binom{5}{2} = 10\)
- \(C_A = 2/10 = 0.2\)
What are the local clustering coefficients of A, B and C?
\[ C_i = \dfrac{\text{# of triangles involving } i \text{ and its neighbors}}{\text{# of edges possibly exist in the neighborhood of } i} \]
- A: \(2/6 = 1/3\)
- B: \(1/3 = 1/3\)
- C: \(0\)
Clustering Coefficient (2)
Average clustering coefficient is the average of the local clustering coefficients of all nodes.
\[ \overline{C} = \dfrac{1}{N} \sum_{i} C_i \]
\[ \overline{C} = \frac{1}{6}\left( \underbrace{\frac{1}{3}}_{A} + \underbrace{\frac{1}{3}}_{B} + \underbrace{0}_{C} + \underbrace{\frac{1}{3}}_{D} + \underbrace{0}_{E} + \underbrace{\frac{2}{3}}_{F} \right) = \frac{5}{18} \]
Clustering Coefficient (3)
Global clustering coefficient focuses on the total number of triangles in the network.
\[ C = \frac{3 \times \text{number of triangles}}{\text{number of connected triplets}} = \frac{3 \times \text{number of triangles}}{\sum_{i} k_i(k_i-1)/2} \]
where \(k_i\) is the degree of node \(i\).
Connected triplets = Three nodes joined by at least two edges. When counting, we distinguish the triplets by the node that is centered. A triangle counts as three triplets. A node with degree \(k\) has \(k(k-1)/2\) triplets.
Three types of clustering coefficients:
Local clustering coefficient \(\rightarrow\) Density of triangles in a node’s neighborhood
Average clustering coefficient \(\rightarrow\) Average of the local clustering
Global clustering coefficient \(\rightarrow\) Density of triangles in the entire network
Question:
If a network has a high global clustering coefficient, does it necessarily have a high average local clustering coefficient?
If not, can you draw a network with high global clustering but low average local clustering coefficient?
Average Path Length (1)
Now, let’s quantify the global connectivity via the average path length.
Distance between two nodes \(i\) and \(j\) is the minimum number of edges you need to traverse to get from one node to the other
Let’s find the distance between A and D:
- Path 1: A \(\rightarrow\) B \(\rightarrow\) D (2 edges)
- Path 2: A \(\rightarrow\) C \(\rightarrow\) D (2 edges)
- Path 3: A \(\rightarrow\) C \(\rightarrow\) B \(\rightarrow\) D (3 edges)
Even though there are multiple paths, the distance from A to D is 2 edges.
Average Path Length (2)
Average path length \(L\) is the average distance between any two nodes:
\[ \overline{L} = \frac{2}{N(N-1)} \sum_{i<j} d_{ij} \]
where \(d_{ij}\) is the shortest path length between node \(i\) and node \(j\), and \(N\) is the number of nodes in the network.
\[ \begin{aligned} L &= \frac{1}{6} \left( \underbrace{1}_{A-B} + \underbrace{1}_{A-C} + \underbrace{2}_{A-D} + \underbrace{1}_{B-C} + \underbrace{1}_{B-D} + \underbrace{1}_{C-D} \right) \\ &= \frac{7}{6} \simeq 1.16 \end{aligned} \]
Small-world networks are networks that have both high clustering coefficient and short average path length.
And we can quantify the “small-worldness” of a network by, for example,
\[ \sigma_{\text{naive}} = \dfrac{\text{average clustering coefficient}}{\text{average path length}} \]
- But there is a problem 🤔
- Both clustering coefficient and average path length are correlated with the number of nodes \(N\) and edges \(M\).
- Example: A small network has short average path length. Dense network has high clustering.
- Let’s control for the effect of the number of nodes \(N\) and edges \(M\).
- Think about rewiring the edges of the network randomly—this is called Erdős-Rényi random graph.
- This random network has the same number of nodes and edges but would have a different \(\sigma_{\text{naive}}\) value.
- Denoted by \(\sigma_{\text{random}}\) the average of \(\sigma_{\text{naive}}\) over many random networks.
- We normalize \(\sigma_{\text{naive}}\) by \(\sigma_{\text{random}}\): \[ \sigma = \dfrac{\sigma_{\text{naive}}}{\sigma_{\text{random}}} \]
- If \(\sigma > 1\), the network is small-world more than random networks.
Small-world Coefficient
\[ \sigma = \dfrac{\sigma_{\text{naive}}}{\sigma_{\text{random}}} \]
- \(\sigma > 1\): Strong small-world property
- \(\sigma \approx 1\): Comparable to random network
- \(\sigma < 1\): Anti-small-world
For Erdős-Rényi Random Graphs, we have:
\[ \sigma_{\text{random}} = \dfrac{\overline{C}_{\text{random}}}{\overline{L}_{\text{random}}},\quad \overline{C}_{\text{random}} \approx \dfrac{\langle k \rangle}{N-1},\quad \overline{L}_{\text{random}} \approx \dfrac{\ln N}{\ln \langle k \rangle} \]
where \(\langle k \rangle\) is the average degree. See the lecture note for the derivation.
Now, we have a way to quantify the small-worldness of a network.
But we still don’t know why small-world networks emerge.
“What I cannot create, I do not understand”
—Richard Feynman
What are the mechanism behind the small-world phenomenon 🤔?

The Watts-Strogatz Model
Step 1: Create ring of \(N\) nodes connected to \(k\) nearest neighbors
- High clustering, long paths
Step 2: Randomly rewire each edge with probability \(p\)
- \(p = 0\): regular lattice
- \(p = 1\): random graph
- \(0 < p < 1\): small-world
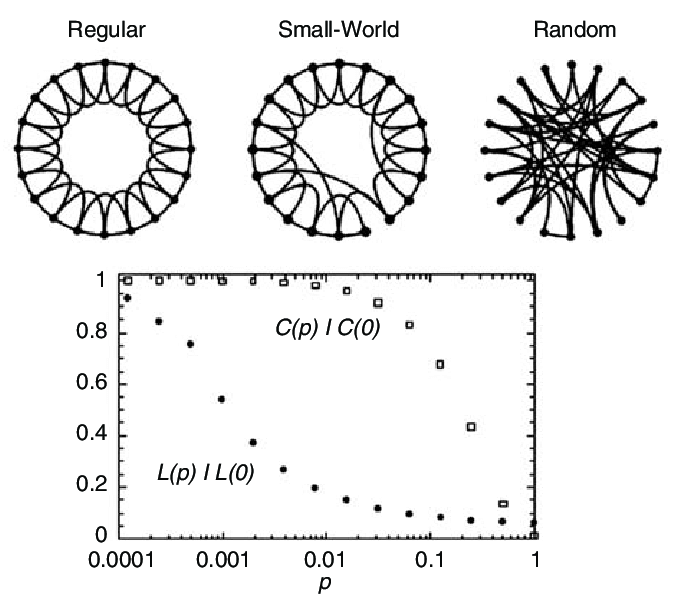
Why Small-World Emerges
The Mechanism:
- Start with local clustering (ring lattice)
- Add a few long-range connections (rewiring)
- These “shortcuts” dramatically reduce path lengths
- Maintains high clustering while creating short paths
Examples:
- Biological networks: Neurons with local + long-range connections
- Technological networks: Internet with regional + continental links
- Social networks: Local friends + distant acquaintances
Key Takeaways
- Small-world networks combine high clustering with short path lengths
- Milgram’s experiment revealed “six degrees of separation”
- Watts-Strogatz model explains the mechanism through edge rewiring
- Quantification possible through clustering coefficients and path lengths
- Long-range connections are key to the small-world phenomenon
Next: We’ll learn to compute shortest paths and connected components using igraph
Convenient libraries for network analysis
- networkx - a beginner-friendly library for network analysis
- igraph - a mature library with a wide range of algorithms
- graph-tool - specialized for stochastic block models
- scipy - efficient tools for analyzing large networks
Throughout this course, we’ll primarily use igraph, a mature and robust library originally developed for R and later ported to Python.
Let’s code! 🚀
First Step: Choose a notebook to work on
Marimo:
https://github.com/skojaku/adv-net-sci/notebooks/m02-small-world/starter.py
Open the terminal and run:
or via uv
Jupyter Notebook:
https://github.com/skojaku/adv-net-sci/notebooks/m02-small-world/starter.ipynb
Toy network
import igraph
edge_list = [(0, 1), (1, 2), (0, 2), (0, 3)]
g = igraph.Graph() # Create an empty graph
g.add_vertices(4) # Add 4 vertices
g.add_edges(edge_list) # Add edges to the graphPlot the graph.
Path
Simple paths:
Shortest path:
Distance:
Connected Components
Find connected components:
Membership:
Size:
The largest connected component:
Clustering coefficient
Local clustering coefficient:
Average clustering coefficient:
Global clustering coefficient:
Watts-Strogatz Model
n_ws = 30 # Number of nodes
k_ws = 6 # Number of nearest neighbors in the ring lattice
p_rewire = 0.1 # Probability of rewiring each edge
g_smallworld = igraph.Graph.Watts_Strogatz(
dim=1,
size=n_ws,
nei=k_ws // 2,
p=p_rewire,
)Compute the small-worldness \(\sigma\) using the formula below:
\[ \sigma = \dfrac{\sigma_{\text{naive}}}{\sigma_{\text{random}}}, \; \text{where}\; \sigma_{\text{naive}} = \dfrac{\text{average clustering coefficient}}{\text{average path length}} \]
\[ \sigma_{\text{random}} = \dfrac{\overline{C}_{\text{random}}}{\overline{L}_{\text{random}}},\; \overline{C}_{\text{random}} \approx \dfrac{\langle k \rangle}{N-1},\; \overline{L}_{\text{random}} \approx \dfrac{\ln N}{\ln \langle k \rangle} \]
What’s Next?
Module 03: Network Robustness
Does a network remain connected when one or more nodes fail?
