import igraph as ig
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
A = ig.Graph.Famous("Zachary").get_adjacency_sparse() # Load the karate club network
eigvals, eigvecs = np.linalg.eig(A.toarray()) # Eigenvalues and eigenvectors
eigvals, eigvecs = np.real(eigvals), np.real(eigvecs)
fig, axes = plt.subplots(1,4, figsize=(15,3))
for i in range(3):
u = eigvecs[:, i].reshape((-1,1))
lam = eigvals[i]
basisMatrix = u @ u.T
sns.heatmap(basisMatrix, ax=axes[i+1], cmap="coolwarm", center=0)
axes[i+1].set_title(f"Lambda={lam:.2f}")
sns.heatmap(A.toarray(), ax=axes[0], cmap="coolwarm", center=0)
axes[0].set_title("Adjacency Matrix")
plt.show()Solution for general d dimensional case
Check list
Slide 08: Network Embedding
Sadamori Kojaku
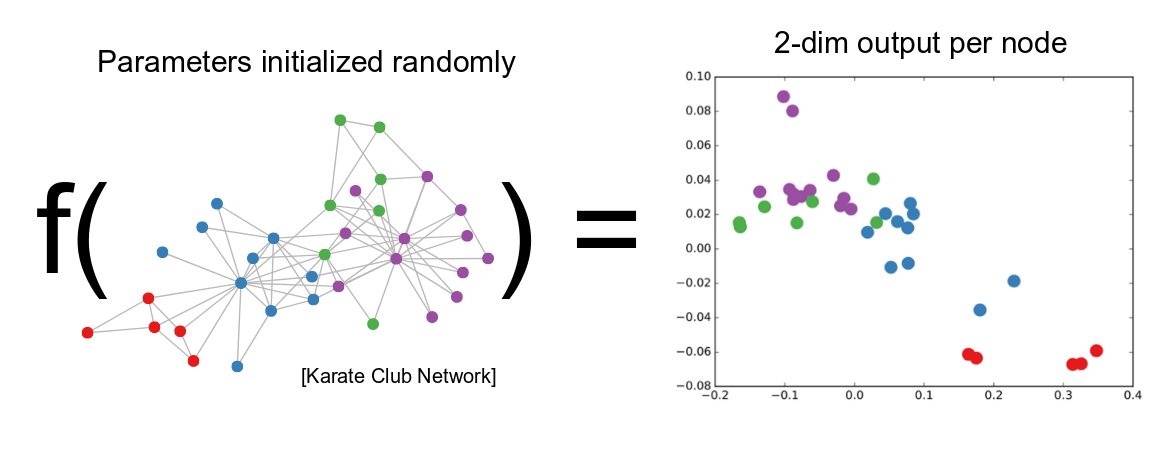
Network Embedding 🌐
- Task: Embed a network into a low-dimensional vector space
- Embedding can recover the network with high accuracy
- Embedding should be low-dimensional
Question:
How would you do that? What approaches would be viable?
Pen and Paper ✍️
Idea 1: Network reconstruction
Compress adjacency matrix A into low-dim representation U that minimizes the reconstruction error:
\min \frac{1}{2}||\mathbf{A} - \lambda \mathbf{U}\mathbf{U}^\top||_F^2
where
U = \begin{bmatrix} | & | & & | \\ \mathbf{u}_1 & \mathbf{u}_2 & \cdots & \mathbf{u}_d \\ | & | & & | \end{bmatrix} \in \mathbb{R}^{n \times d}, \quad \mathbf{u}^\top_i \mathbf{u}_j = 0 \quad \forall i \neq j, \text{and} \quad \sum_i u_i^2 = 1
Question:
Try solving this for the 1d case (only u_1)
Proof sketch
\frac{1}{2}||\mathbf{A} - \lambda \mathbf{U}\mathbf{U}^\top||_F^2 = \frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N (A_{ij} - \lambda u_i u_j)^2
This is a convex function of u_i. Meaning that the gradient is 0 at the minimum. Thus, by taking derivative with respect to u_i, we can find the optimal u_i by solving the following equation:
\frac{\partial}{\partial u_i}\left[ \frac{1}{2}\sum_{i=1}^N \sum_{j=1}^N (A_{ij} - \lambda u_i u_j)^2 \right] = 0
Deriving the solution
By setting the derivative to 0, we get:
\begin{align} \frac{\partial}{\partial u_i}\left[ \frac{1}{2}\sum_{i=1}^N \sum_{j=1}^N (A_{ij} - \lambda u_i u_j)^2 \right] &= \underbrace{2}_{\text{Why🤔?}} \times \left[ \sum_{j=1, j\neq i}^N (A_{ij} - \lambda u_i u_j)(-\lambda u_j)\right] + (A_{ii} - \lambda u_i^2) (-2\lambda u_i) = 0 \\ &\iff -2 \lambda \left[ \sum_{j=1, j\neq i}^N A_{ij}u_j - \lambda^2 u_i u_j^2 \right] - 2 \lambda A_{ii}u_i + 2\lambda^2 u_i^3 \\ &\iff \sum_{j=1}^N A_{ij}u_j - \lambda u_i \underbrace{\sum_{j=1}^N u_j^2}_{=1 \text{ (our constraint)}}\\ &\iff \sum_{j=1}^N A_{ij}u_j = \lambda u_i \end{align}
Eigenvalue problem
This is an eigenvalue problem of A, i.e.,
\mathbf{A} \mathbf{u} = \lambda \mathbf{u}
Question:
But we have N eigenvectors (u_i) with 0 gradient. Which one should we choose?
Which eigenvector should we choose?
A guiding criterion is the reconstruction error, i.e., choose the eigenvector with eigenvalue \lambda that minimizes the reconstruction error.
\frac{1}{2}||\mathbf{A} - \lambda \mathbf{u}\mathbf{u}^\top||_F^2 = \text{Tr}((\mathbf{A} - \lambda \mathbf{u}\mathbf{u}^\top)^\top (\mathbf{A} - \lambda \mathbf{u}\mathbf{u}^\top))
Hint: Let’s use the matrix Frobenius norm:
||\mathbf{M}||_F^2 = \text{Tr}(\mathbf{M}^\top\mathbf{M})
And see how it relates to the eigenvalue.
Finding the optimal eigenvalue
Expanding it gives
\begin{align} \text{Tr}((\mathbf{A} - \lambda \mathbf{u}\mathbf{u}^\top)^\top (\mathbf{A} - \lambda \mathbf{u}\mathbf{u}^\top)) &= \underbrace{\text{Tr}(\mathbf{A}^\top\mathbf{A})}_{\text{const.}} - 2\lambda \text{Tr}(\mathbf{u}^\top\mathbf{A}\mathbf{u}) + \lambda^2 \underbrace{\text{Tr}(\mathbf{u}^\top\mathbf{u}\mathbf{u}^\top\mathbf{u})}_{\text{const. (why? 🤔)}}) \\ &\propto -2 \lambda \underbrace{\text{Tr}(\mathbf{u}^\top\mathbf{A}\mathbf{u})}_{\text{$=\lambda$ (why? 🤔)}} \end{align}
Altogether, the reconstruction error is
\frac{1}{2}||\mathbf{A} - \lambda \mathbf{u}\mathbf{u}^\top||_F^2 = - \lambda^2 + \text{const.}
It is minimized when \lambda is the largest eigenvalue. So the best u is the eigenvector corresponding to the largest eigenvalue.
Why eigenvectors?
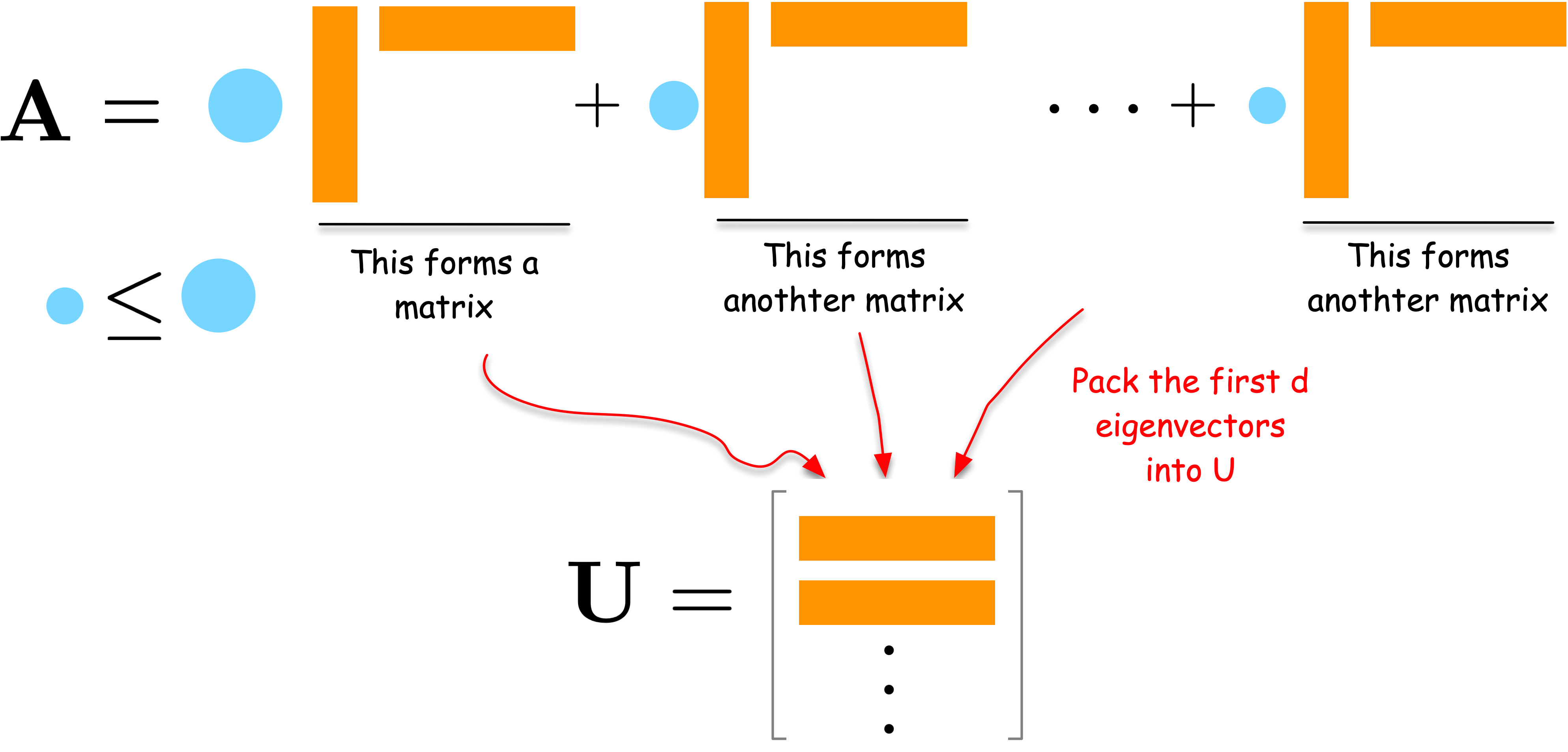
Intuition behind eigenvectors

The d eigenvectors associated with the largest d eigenvalues give the optimal solution that minimizes the reconstruction error for the d dimensional case.
Fed up with the math? Let’s try it out! 🧑💻
import numpy as np
import igraph as ig
A = ig.Graph.Famous("Zachary").get_adjacency_sparse() # Load the karate club networkTask 1: Compute the eigenvectors and eigenvalues of A.
Task 2: Compute the sum of reconstructed matrices using the first d eigenvectors for d=1,2,3,4,5 and compare it with the original adjacency matrix A.
\frac{1}{2}||\mathbf{A} - \sum_{i=1}^d \lambda_i \mathbf{u}_i \mathbf{u}_i^\top||_F^2
where u_i is the eigenvector corresponding to the i-th largest eigenvalue \lambda_i.
Let’s try it out more!
The adjacency matrix is not the only matrix that represents a network.
What do the eigenvectors of the following matrices look like? Compute the eigenvectors, visualize them (e.g., heatmap) and see what they are likely to represent.
- Laplacian matrix L = D - A, where D is the degree matrix.
- Normalized Laplacian matrix L_n = I - D^{-1/2} A D^{-1/2}.
Work with Zachary’s karate club network.
Idea 2: Graph Cut ✂️
Graph cut Problem
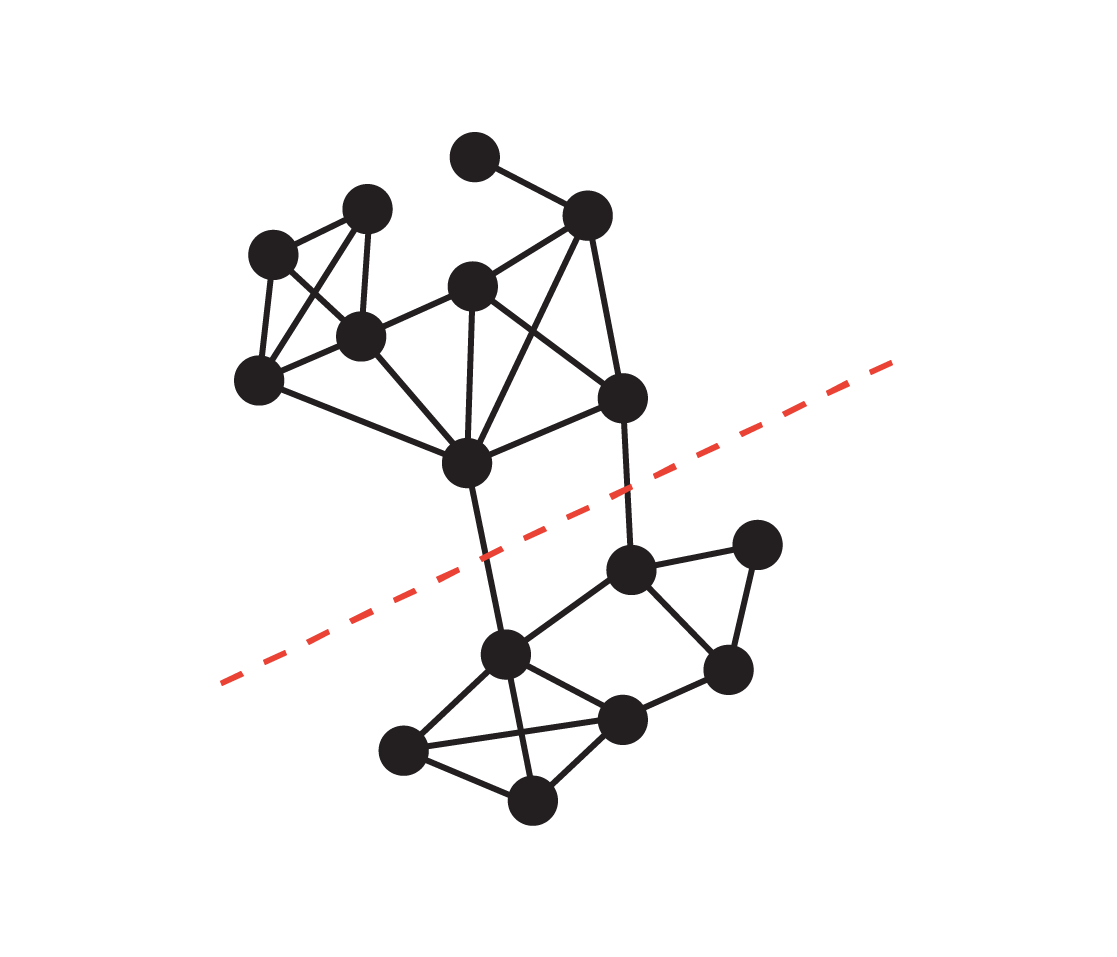
Graph cut Problem ✂️
Disconnect a graph into two components by cutting the minimum number of edges
\min_{Q,S} \text{cut}(Q,S) = \sum_{i \in Q} \sum_{j \in S} A_{ij}
where |Q \cup S| = N, \quad Q \cap S = \emptyset
This has a close relationship with the Laplacian matrices L and L_n given by
L = D - A, \quad L_n = I - D^{-1/2} A D^{-1/2}
where D is the degree matrix and A is the adjacency matrix.
Ratio Cut
Ratio Cut:
\sum_{i \in Q} \sum_{j \in S} A_{ij} \left( \frac{1}{|Q|} + \frac{1}{|S|} \right) = \frac{1}{N} \mathbf{x}^\top \mathbf{L} \mathbf{x}
where L = D - A (the combinatorial Laplacian matrix) with {\bf x}=[x_1,x_2,...,x_N]^\top is an indicator vector for the partition.
x_i = \begin{cases} \sqrt{|S|/|Q|} & \text{if } i \in Q \\ -\sqrt{|Q|/|S|} & \text{if } i \in S \end{cases}
x_i appears to be peculiar but has convenient properties, i.e., zero mean and normalization, i.e.,
\sum_i x_i = 0, \quad \sum_i x_i^2 = N
Let’s prove this!
Deriving the Ratio Cut formula
Consider distance between points x_i and x_j:
(x_i - x_j)^2 = \left(\sqrt{\frac{|S|}{|Q|}} + \sqrt{\frac{|Q|}{|S|}}\right)^2 = \frac{|S|^2 + |Q|^2 + 2|S||Q|}{|Q||S|} = \frac{(|S| + |Q|)^2}{|Q||S|} = \frac{N^2}{|Q||S|}
\begin{align} \text{RatioCut}(Q,S) &= \sum_{i \in Q} \sum_{j \in S} A_{ij} \left( \frac{1}{|Q|} + \frac{1}{|S|} \right) = \sum_{i \in Q} \sum_{j \in S} A_{ij} \left( \frac{|Q| + |S|}{|Q||S|} \right) \\ &= \frac{1}{N}\sum_{i \in Q} \sum_{j \in S} A_{ij} \left( x_i - x_j \right)^2 \\ &= \frac{1}{2N}\underbrace{\sum_{i=1}^N \sum_{j=1}^N}_{\text{Sum over all node pairs.}} A_{ij} \left( x_i - x_j \right)^2 \end{align}
(The last equality holds because (x_i - x_j)^2 = 0 for i,j \in Q or i,j \in S.)
Connecting to Laplacian
By expanding the square term, we get
\begin{align*} \text{RatioCut}(Q,S) &= \frac{1}{2N}\sum_{i=1}^N \sum_{j=1}^N A_{ij} \left( x_i - x_j \right)^2 \\ &= \frac{1}{N}\sum_{i=1}^N x^2_i \underbrace{\sum_{j=1}^N A_{ij}}_{\text{degree } k_i} - \frac{1}{N}\sum_{i=1}^N \sum_{j=1}^N A_{ij} x_i x_j \\ &= \frac{1}{N}\sum_{i=1}^N k_i x^2_i - \frac{1}{N}\sum_{i=1}^N \sum_{j=1}^N A_{ij} x_i x_j \\ &= \frac{1}{N}\sum_{i=1}^N \sum_{j=1} ^N L_{ij} x_i x_j \\ \end{align*}
Therefore,
\text{RatioCut}(Q,S) = \frac{1}{N} \mathbf{x}^\top \mathbf{L} \mathbf{x}.
The optimization problem
The ratio cut minimization problem is formulated as
\min_{\mathbf{x}} \mathbf{x}^\top \mathbf{L} \mathbf{x}
subject to
\mathbf{x} \mathbf{1} = 0, \quad \mathbf{x}^\top \mathbf{x} = N \quad x_i \in \left\{\sqrt{|S|/|Q|}, -\sqrt{|Q|/|S|}\right\}
This is an NP-hard problem 😿. But, there is a way to get a good suboptimal solution by using spectral embedding!
💫 Core idea 💫: Relax the discrete constraint by allowing x_i to be any real number. But keep the normalization constraint:
\mathbf{x}^\top \mathbf{1} = 0, \quad \mathbf{x}^\top \mathbf{x} = 1 \quad x_i \in [-1,1]
Question:
What is the solution to this optimization problem?
Solution via eigenvalue problem
Consider the eigenvalue problem:
\mathbf{L} \mathbf{x} = \lambda \mathbf{x}
By applying x to both sides, we get
\mathbf{x}^\top \mathbf{L} \mathbf{x} = \lambda \mathbf{x}^\top \mathbf{x} = \lambda
where we have used ||x|| = 1. The left-hand side is exactly the objective function we want to minimize!
Thus the solution is the eigenvector corresponding to the smallest eigenvalue 😉….
import numpy as np
import igraph as ig
A = ig.Graph.Famous("Zachary")
.get_adjacency_sparse() # LoadCompute the combinatorial Laplacian matrix L given by
\mathbf{L} = \mathbf{D} - \mathbf{A}
where D is the degree matrix.
Task 1: Compute the eigenvector associated with the smallest eigenvalue of L and visualize it.
Task 2: Compute the second smallest eigenvector and plot it.
Issue with the “best” solution
Thus the solution is the eigenvector corresponding to the smallest eigenvalue 😉.
The eigenvector corresponding to the smallest eigenvalue is parallel to the all-ones vector.
\mathbf{x}_1 = \frac{1}{\sqrt{N}} \begin{bmatrix} 1 & 1 & \cdots & 1 \end{bmatrix}^\top
which violates the zero mean constraint:
\mathbf{x}^\top \mathbf{1} = 0
The second smallest eigenvector is orthogonal to x_1.
- This is because the eigenvectors are orthogonal to each other.
- Thus, the solution is the eigenvector corresponding to the second smallest eigenvalue!
- The second, and third, and … smallest eigenvectors can be used to get a k-way partition of the network.
Normalized Cut
Let us derive another spectral embedding method based on the normalized cut.
\text{NC}(Q,S) = \frac{\text{cut}(Q,S)}{\text{vol}(Q)} + \frac{\text{cut}(Q,S)}{\text{vol}(S)}
where
\text{vol}(Q) = \sum_{i \in Q} k_{i}, \text{vol}(S) = \sum_{i \in S} k_{i}
The objective is expressed as:
z^\top L_n z
where z is an indicator vector given by
z_i = \begin{cases} \sqrt{\frac{\text{vol}(S)}{\text{vol}(Q)}} & \text{if } i \in Q \\ -\sqrt{\frac{\text{vol}(Q)}{\text{vol}(S)}} & \text{if } i \in S \end{cases}
And L_n is the normalized Laplacian matrix given by
\mathbf{L}_n = \mathbf{I} - \mathbf{D}^{-1/2} \mathbf{A}\mathbf{D}^{-1/2}
Prove it!
Laplacian Eigenmap 🔄
Objective: Position connected nodes close together
\min_{\mathbf{u}} \sum_{i,j} A_{ij} (\mathbf{u}_i - \mathbf{u}_j)^2
Question:
What is the solution to this optimization problem?
Neural Embedding Methods
Neural networks for embedding
How can I apply neural networks to embedding?
- Run random walks
- Treat the walks as sentences
- Apply neural networks to predict temporal correlations between words
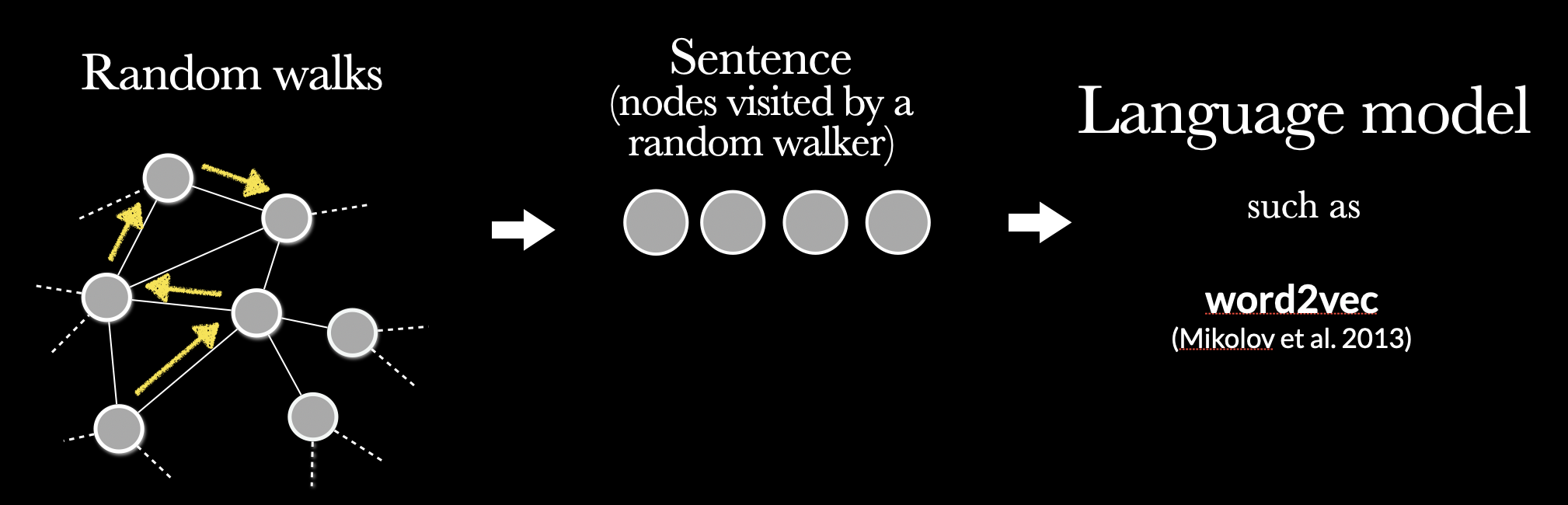
DeepWalk & node2vec: Use word2vec to learn node embeddings from random walks
Note:
This is one way. Another popular way is to use convolution inspired from image processing.
CBOW Model
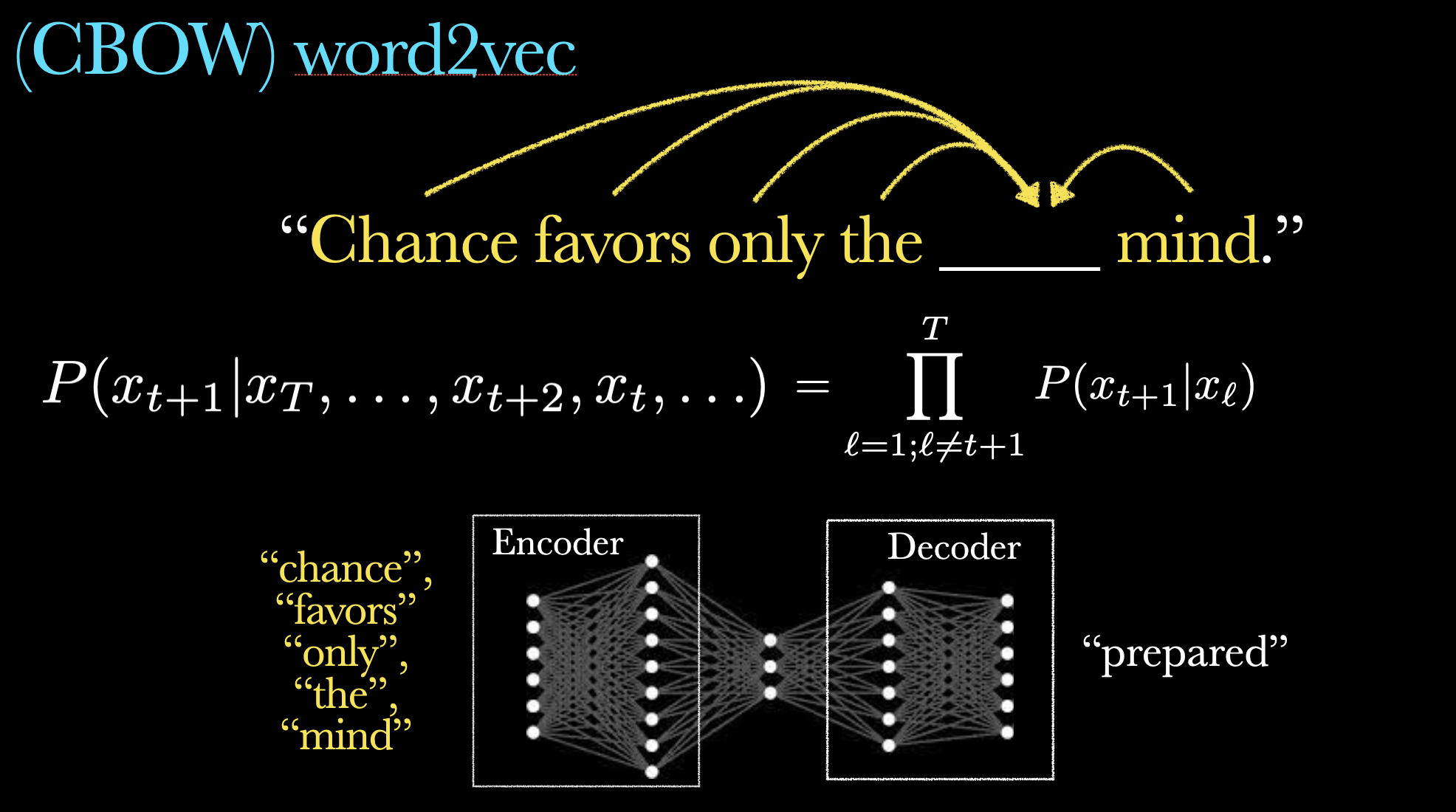
Skipgram
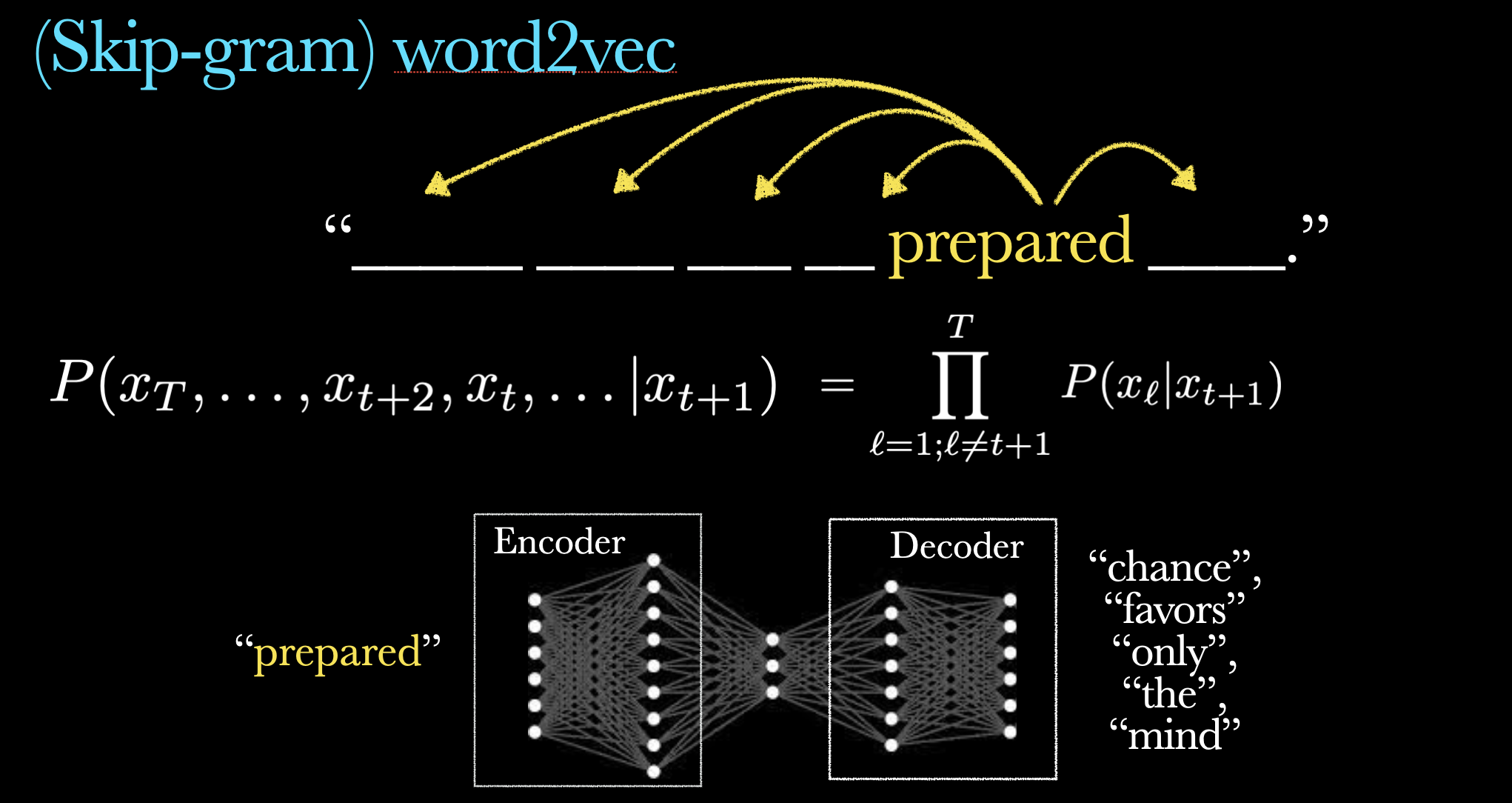
node2vec 📝

- Learn multi-step transition probabilities of random walks
- High probability ~ close in the embedding space
Note:
Precisely speaking, this is not an accurate model description. node2vec is trained on a biased training algorithm. Consequently, two frequently co-visited nodes are not always embedded closely. See paper
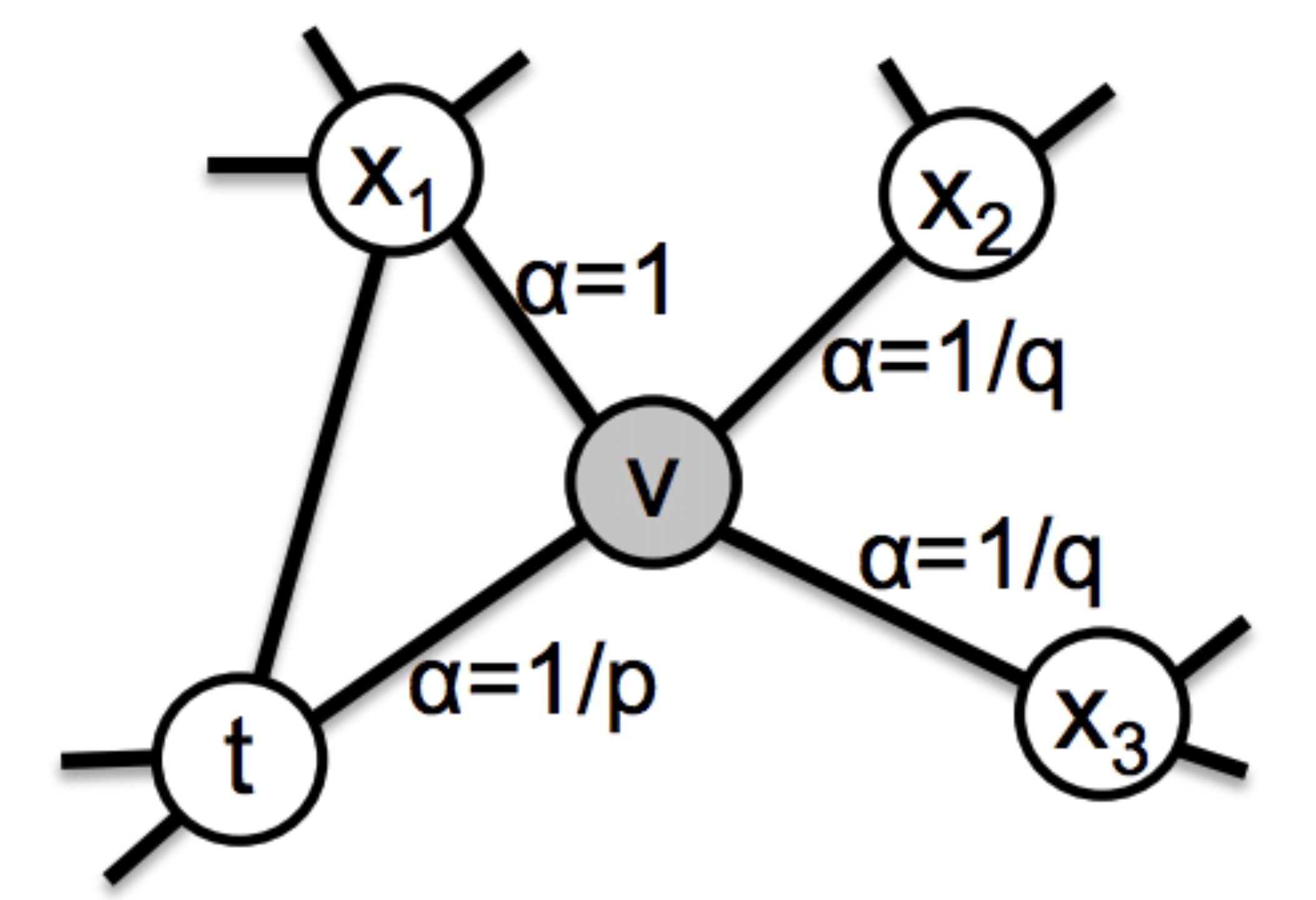
node2vec random walks
Biased Random Walk:
\begin{align*} P(x_{t+1}|x_t, x_{t-1}) \propto\begin{cases} \frac{1}{p} & \text{Return to } x_{t-1} \\ 1 & \text{Move to a neighbor $x_{t+1}$ directly connected to } x_{t-1} \\ \frac{1}{q} & \text{Move to a neighbor $x_{t+1}$ *not* directly connected to } x_{t-1} \end{cases} \end{align*}
Parameters:
- p: Return parameter (lower = more backtracking)
- q: Exploration parameter (lower = more exploration)
which control the walker to move away from the previous node or stay locally.
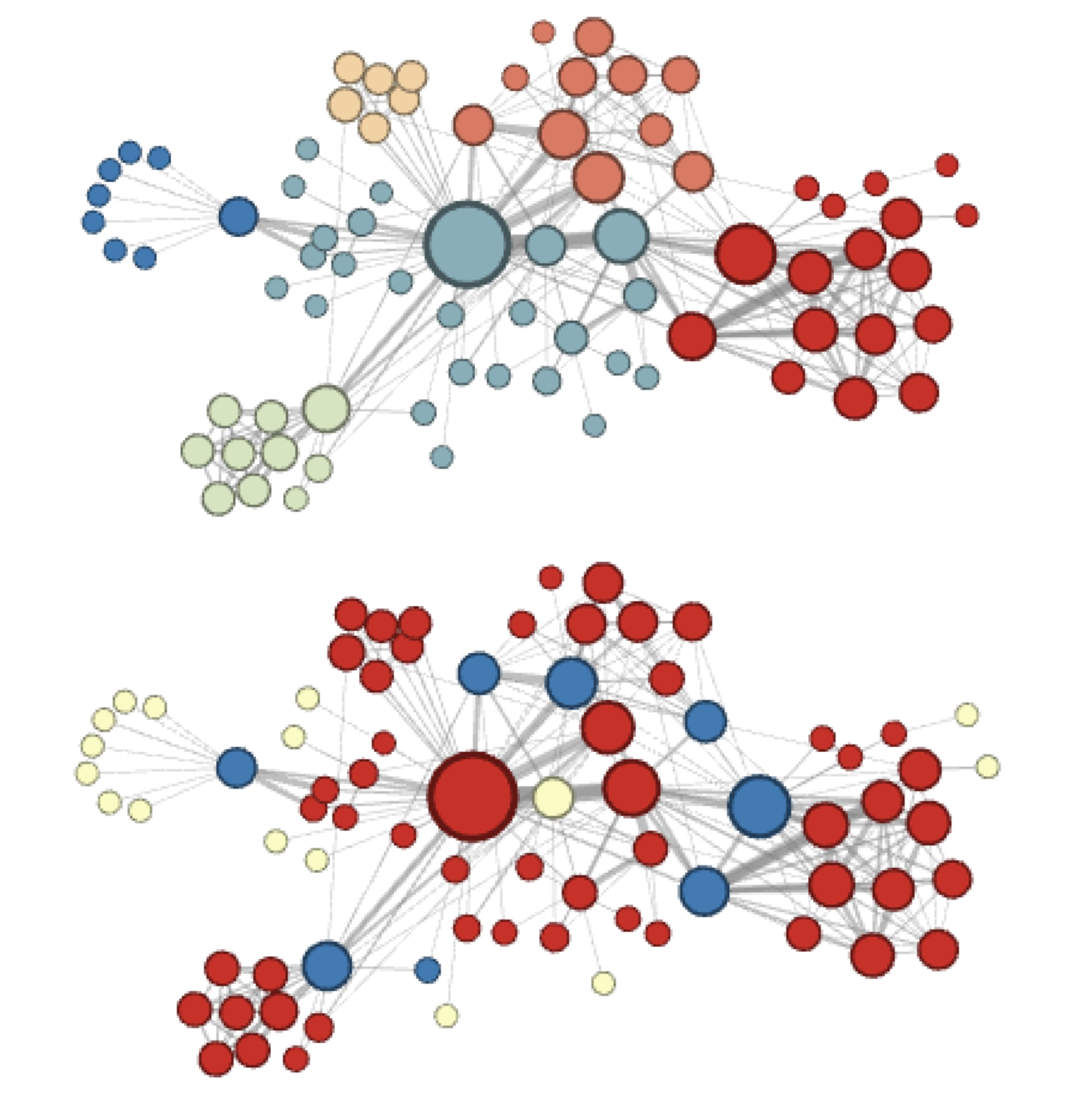
Example: Les Misérables Network 📚
Complementary visualizations of Les Misérables coappearance network generated by node2vec with label colors reflecting homophily (top) and structural equivalence (bottom).
Let’s try it out!
Hyperbolic Embedding Methods
Let’s think about geometry… 🌍
Question:
All the embedding methods we’ve seen so far use Euclidean space (flat geometry).
But what if our network has a hierarchical structure—like a tree or organization chart?
Can flat space efficiently capture exponentially growing hierarchies?
Take 30 seconds to think about it…
The Challenge with Euclidean Space
- Problem: Real networks have
- Hierarchical structures
- Scale-free properties
- Strong clustering + small-world
- Issue: In flat (Euclidean) space, volume grows polynomially with radius
- But: Tree-like hierarchies grow exponentially
- This is a fundamental mismatch!
What is Hyperbolic Space?
Hyperbolic geometry = curved space with negative curvature
Key Property:
Volume grows exponentially with radius—just like trees!
This naturally captures:
- Scale-free degree distributions
- Strong clustering
- Small-world property
- Self-similarity
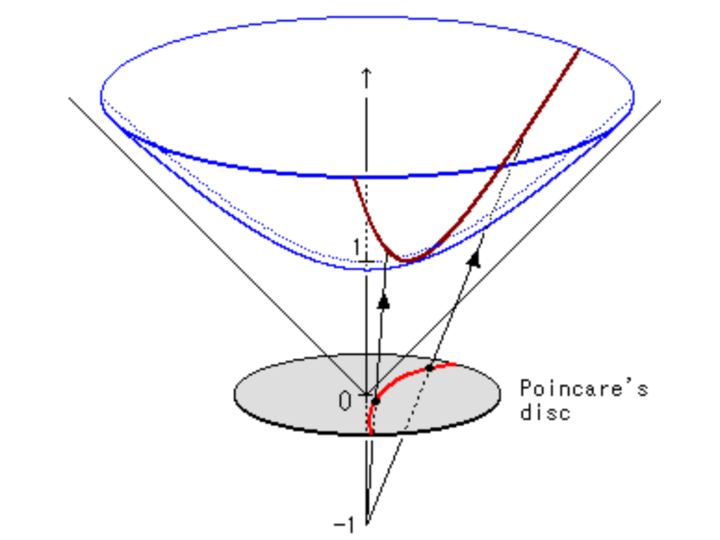
Poincaré disk: hyperbolic space visualized in a circle
The Popularity-Similarity Framework
How do real networks actually grow? 🤔
Question:
2012: Researchers analyzed Internet, metabolic, and social networks
Do new nodes just connect to popular nodes (preferential attachment)?
Or is there something more going on? Think about a case (e.g., social network, transportation network, etc.) where it is not the case.
Answer: It’s Both! ⚖️
Discovery:
Networks grow by balancing two factors:
- Popularity: Connect to well-established nodes
- Similarity: Connect to similar nodes
This optimization naturally emerges in hyperbolic space!
- Popularity → radial position (birth time)
- Similarity → angular distance
- New connections → hyperbolically closest nodes
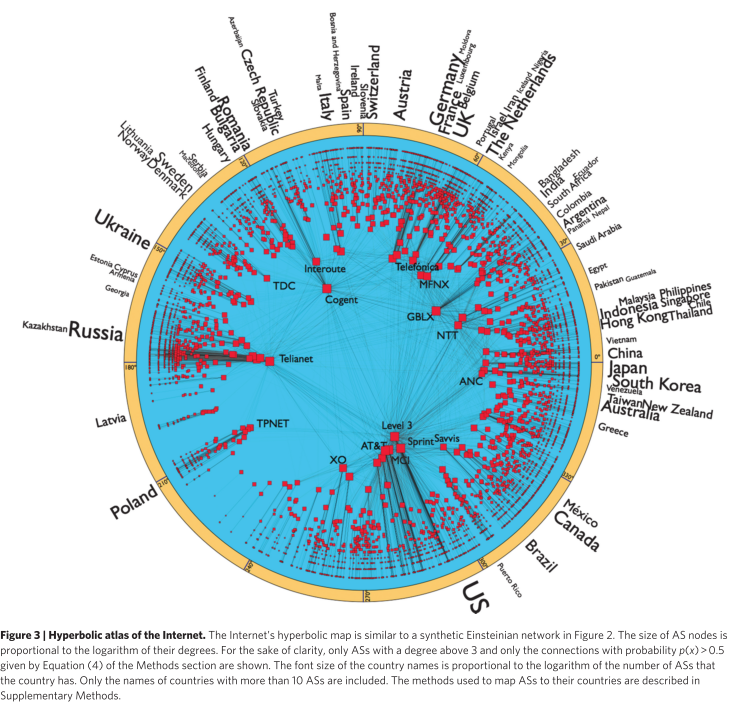
How does the model actually work? 🔧
Question:
If networks grow by balancing popularity and similarity, what are the precise rules?
How do we generate a network that captures this?
Let’s break down the mathematical rules…
The Core Model: Popularity × Similarity
Network Generation Process:
- At each time t = 1, 2, 3, \dots, add a new node t
- Each node t gets coordinates:
- Random angular position on a circle, \theta_t
- Radial position based on birth time, r_t = \ln t (older = more popular)
- New node t connects to the m nodes that minimize:
s \cdot \theta_{st} \quad \text{for } s < t
Key property: In this space, the rule “minimize s \cdot \theta_{st}” is mathematically equivalent to connecting to the m hyperbolically closest nodes.

The Connection Rule: Balancing Two Forces ⚖️
Key insight:
- The number of nodes to connect to depends on both popularity and similarity
- If a node is very popular, it should connect to many nodes
- If a node is surrounded by many similar nodes, it should connect to many nodes
- The
radiusof the node is often referred to as theimplicitdegree.- Example: European airports have high degree in part becaues there are many airports in Europe. Their implicit degree might be lower than what the degree suggests.
- Preferential attachment is not a primitive mechanism
- Probability \Pi(k) \propto k emerges naturally
- It’s a consequence of geometric optimization!
Mathematical Models of Hyperbolic Space
Two Ways to Represent Hyperbolic Space
Question:
How can we mathematically represent this curved space in a computer?
We have two main models (they’re mathematically equivalent but computationally different):
1. Poincaré Ball Model 🔮
Points lie within unit ball: \|\mathbf{x}\| < 1
Distance formula:
d_P(\mathbf{u}, \mathbf{v}) = \text{arcosh}\left(1 + 2\frac{\|\mathbf{u} - \mathbf{v}\|^2}{(1 - \|\mathbf{u}\|^2)(1 - \|\mathbf{v}\|^2)}\right)
Properties:
- Intuitive visualization
- Geodesics = circular arcs
- Requires complex Riemannian optimization
Shapes appear to shrink near boundary, but they’re all the same hyperbolic size!
2. Lorentzian (Hyperboloid) Model 🎯
Points lie on hyperboloid in Minkowski space
Lorentzian inner product:
\langle\mathbf{x}, \mathbf{y}\rangle_L = -x_0 y_0 + x_1 y_1 + \cdots + x_n y_n
Distance formula:
d_L(\mathbf{u}, \mathbf{v}) = \text{arcosh}(-\langle\mathbf{u}, \mathbf{v}\rangle_L)
Advantage: More efficient optimization (gradients in Euclidean ambient space)

Hyperboloid projects onto Poincaré disk
Hyperbolic Embeddings in Practice
What do hyperbolic embeddings look like?
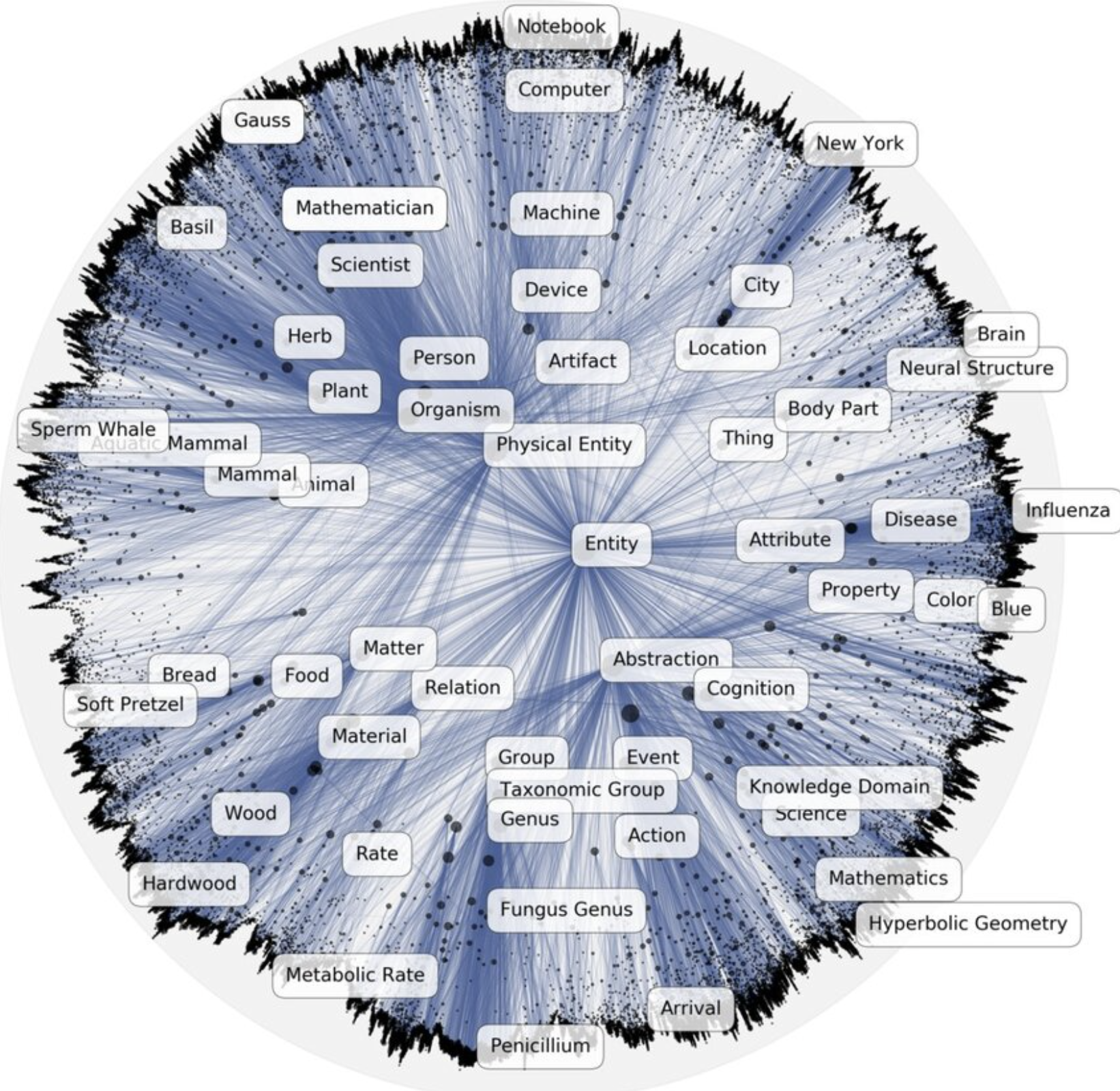
Natural Hierarchy Emerges! 🌳
- Center: Abstract terms (“Entity”, “Object”)
- Moving outward: Increasingly specific
- “Material” → “Wood” → “Hardwood”
- Key insight: Hyperbolic space automatically organizes concepts hierarchically
- No explicit supervision needed!
Why This Works:
The exponential volume growth in hyperbolic space naturally accommodates the exponentially growing number of specific concepts at lower hierarchy levels