Module 03: Network Robustness

Advanced Topics in Network Science

Sadamori Kojaku

skojaku@binghamton.edu

Good LLM questions for Starter Assignment:

• https://github.com/sk-classroom/starter-amahury/blob/main/assignment/quiz.toml
• https://github.com/sk-classroom/starter-nedachocolate63/blob/main/assignment/quiz.toml

Clustering Coefficient (3)

Global clustering coefficient focuses on the total number of triangles in the network.

\[ C = \frac{3 \times \text{number of triangles}}{\text{number of connected triplets}} = \frac{3 \times \text{number of triangles}}{\sum_{i} k_i(k_i-1)/2} \]

where \(k_i\) is the degree of node \(i\).

Connected triplets = Three nodes joined by at least two edges. When counting, we distinguish the triplets by the node that is centered. A triangle counts as three triplets. A node with degree \(k\) has \(k(k-1)/2\) triplets.

Closed triplet (left) and open triplet (right)

Quiz:

• Compute the global clustering coefficient and the average path length of the following network.

• Let’s define the ratio of the clustering coefficient to the average path length as the small-worldness index. What is the problem with this definition?

Learning Objectives

• MST: Minimum spanning trees and network design
• Robustness: Random failures vs. targeted attacks
• Theory: Percolation theory and connectivity
• Design: Robust networks balancing efficiency and resilience

Keywords: MST, Kruskal’s algorithm, Prim’s algorithm, percolation, R-index, robustness paradox

Pen & Paper Exercise

Part I: Minimum Spanning Tree

Post-WWI Czechoslovakia Challenge

• Connect all towns with electricity
• Limited resources for infrastructure
• Minimize cable length
• First systematic solution by Otakar Borůvka (1899-1995)

❓ Question: How would you connect all towns with the minimum total cable length?

Take 30 seconds to think about your approach…

💡 Key Insight

Key Insight: We need a tree that connects all nodes with minimum total weight.

Why a tree?

• No redundant connections (cycles)
• Every node connected exactly once
• Minimum possible edges for full connectivity

Red edges form a tree. Dashed edges are redundant.

Minimum Spanning Tree (MST)

A minimum spanning tree (MST) of a weighted network is a tree that:

• Spans all nodes (connects every location)
• Is a tree (no cycles, no redundant loops)
• Has minimum total weight among all spanning trees

🤔 Algorithm Design Question

❓ Question: Given that we want the minimum spanning tree, what strategy would you use to build it?

Think about: Should we start with the cheapest connections? What if adding a cheap connection creates a loop?

💡 The Answer: Kruskal’s Algorithm

Intuition: “Choose cheapest option, avoid wasteful loops”

1. Sort edges by weight (cheapest first)
2. Add edges in order
3. Skip if creates cycle
4. Continue until all connected

Global Perspective: Considers all connections simultaneously

💡 Prim’s Algorithm

Intuition: “Organic growth from starting point”

1. Start from any node (power plant)
2. Find cheapest connection to an unconnected node
3. Add edge, mark node as connected
4. Repeat until all connected

Local Perspective: Builds incrementally from existing network

Kruskal vs. Prim

A demo in lecture notes

💬 Discussion: When do they find the same MST? When not?

Part II: Network Robustness

🤔 The Vulnerability Problem

What happens if a single node in our MST fails?

Think about: How many towns would lose power? What does this mean for real infrastructure?

Cost efficiency ≠ Robustness

💬 Discussion: How would you modify the network to make it more robust? What are the trade-offs between cost and reliability?

Measuring Network Connectivity

\[\text{Connectivity} = \frac{\text{Size of largest component after removal}}{\text{Original network size}}\]

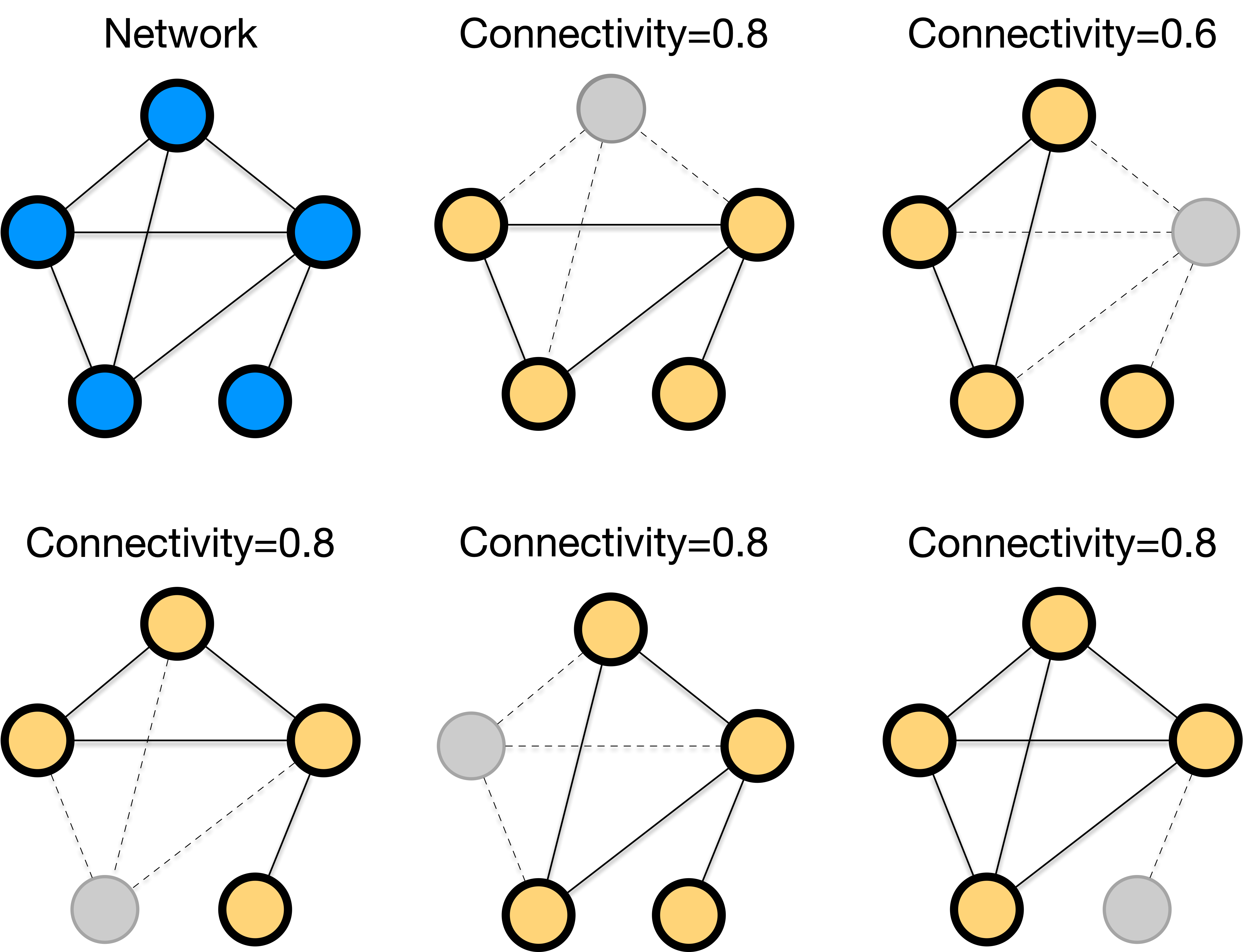
Robustness Profile: Connectivity vs. fraction of nodes removed

R-index: Area under robustness curve \[R = \frac{1}{N} \sum_{k=1}^{N-1} y_k\]

🤔 Attack Strategies

Random Failures:

• Unpredictable events
• Earthquakes, equipment malfunctions
• Technical problems, random server crashes
• Characterized by equal probability of failure for all nodes

Targeted Attacks:

• Strategic node removal by adversaries
• Target busiest airports to disrupt air travel
• Characterized by removing highest-degree nodes, then next highest

Game Time!

Interactive game

• Think about a structure that is robust to random failures/targeted attacks/both

• Why might the same network structure respond so differently to these two scenarios? What does this tell us about network design?

Part III: Theoretical Framework

Percolation Theory

• Suppose puddles are scattered on the ground.
• As rain falls, puddles begin to merge with nearby puddles.
• At first, most puddles are isolated; as more rain falls, clusters form, and eventually a giant puddle spans a large part of the area.

Percolation theory studies how local connections (like merging puddles) lead to sudden global connectivity.

Lecture notes for demonstration

Phase Transition

Critical Point (\(p_c\)): Threshold where giant component emerges/disappears

2D Lattice Example: \(p_c \approx 0.593\)

Lecture notes for demonstration

The sharp transition around \(p_c\) demonstrates a phase transition, i.e., a sudden change from a disconnected to connected state as we cross the critical threshold.

Network Robustness - Where is the critical point?

🤔 Let’s Think Like Network Scientists

Let’s learn how to find the critical point \(p_c \approx 0.593\)

Imagine you’re a node in a network. For you to be a part of the largest connected component, what do you & your friends need 🤔?

• You need friends (connections)
• What else do your friends need?

🔗 Friends of Friends

• Each friend needs at least 2 connections
• One connection: to you
• Another connection: to someone else (to reach the rest of the network)

Your friends need at least 2 friends (on average) for you to be a part of the giant component!

\[ \text{Average \# of friends that friends have} \geq 2 \]

Let’s formalize this insight.

\[ \text{Average \# of friends that friends have} \geq 2 \]

1. Suppose you are node 1 with one hand
2. Other nodes have \(k\) hands with probability \(p(k)\)
3. When you handshake with a randomly picked hand (not node), how many hands do your friends would have on average 🤔?

Suppose \(p(k)\) is the fraction of nodes with \(k\) hands. Altogether, nodes with \(k\) hands contribute \(k p(k)\) hands to the network.

If I randomly pick a hand, I would handshake with a node with \(k\) hands with probability proportional to \(k p(k)\). That is

\[ q(k) = \frac{k p(k)}{\sum_{k=1}^{\infty} k p(k)} = \frac{k}{\langle k \rangle } p(k), \]

where \(\langle k \rangle = \sum_{k=1}^{\infty} k p(k)\) is the average degree. Now, the average number of hands that my friends would have on average is

\[ \langle k \rangle_{q(k)} = \sum_{k=1}^{\infty} k q(k) = \sum_{k=1}^{\infty} k^2 / \langle k \rangle p(k) = \frac{\langle k^2 \rangle}{\langle k \rangle}. \]

🎯 The Molloy-Reed Criterion

You just discovered the Molloy-Reed Criterion! \[\kappa = \frac{\langle k^2 \rangle}{\langle k \rangle} > 2\]

When is the \(\kappa\) smallest 🤔? What is the implication in terms of the robust network structure against random failures?

Take 2 mins to think about it…

• High κ: Hub-dominated networks (some nodes have many friends)
• Low κ: Degree homogeneous networks (everyone has similar friends)
• Implication: Hubs make networks more robust!

🧮 From κ to Critical Fraction

Now let’s figure out: What fraction of nodes can we remove before the network fragments?

Hint: After removing a fraction \(f\) of nodes randomly, what happens to the number of friends a friend would have?

And when does the Molloy-Reed criterion break?

Take 3 mins to think about it.

• After removing fraction \(f\), my friend who initially has—\(\kappa\) friends on average—have \((1-f)(\kappa -1)\) friends on average.
• It’s \(\kappa-1\) not \(\kappa\) because one of the friends is me.
• Thus, the network breaks when \((1-f)(\kappa - 1) = 1\)
• Solving for \(f\), we get \[f_c = 1 - \frac{1}{\kappa - 1}\]

🤔 Case Study: Degree-Homogeneous Networks

Let’s consider a degree-homogeneous network, where the degree distribution is Poisson with mean \(\lambda\), i.e.,

\[ k \sim \mathrm{Poisson}(\lambda) \]

What is the critical point \(f_c\)?

Hint:

• \(f_c = 1 - \frac{1}{\kappa - 1}\), \(\kappa = \frac{\langle k^2 \rangle}{\langle k \rangle}\)
• The mean and variance of the Poisson distribution are identical.

For a Poisson distribution with mean \(\lambda\):

• The first moment (mean degree) is \(\langle k \rangle = \lambda\)
• The second moment is \(\langle k^2 \rangle = \lambda^2 + \lambda\)

Now, we can calculate \(\kappa\):

\[ \kappa = \frac{\langle k^2 \rangle}{\langle k \rangle} = \frac{\lambda^2 + \lambda}{\lambda} = \lambda + 1 \]

Finally, we can find the critical fraction \(f_c\): \[ f_c = 1 - \frac{1}{\kappa - 1} = 1 - \frac{1}{(\lambda + 1) - 1} = 1 - \frac{1}{\lambda} \]

Key Insight: Higher average degree makes the network more robust.

🤔 Case Study: Degree-heterogenous networks

❓ Question: What happens to network robustness when we have a few very highly connected nodes (hubs) and many poorly connected nodes?

Think about: How would random failures affect this type of network? What about targeted attacks?

💡 Robustness of scale-free networks

Let’s consider a scale-free network with the degree distribution:

\[P(k) \sim k^{-\gamma}\]

Infinite variance for \(\gamma < 3\), undefined mean for \(\gamma \leq 2\).

Most real-world networks do not have finite variance!

What does it mean in terms of the robustness of the network?

When the network is infinite,

\(f_c \rightarrow 1\) when \(2 < \gamma < 3\).

When the network is finite,

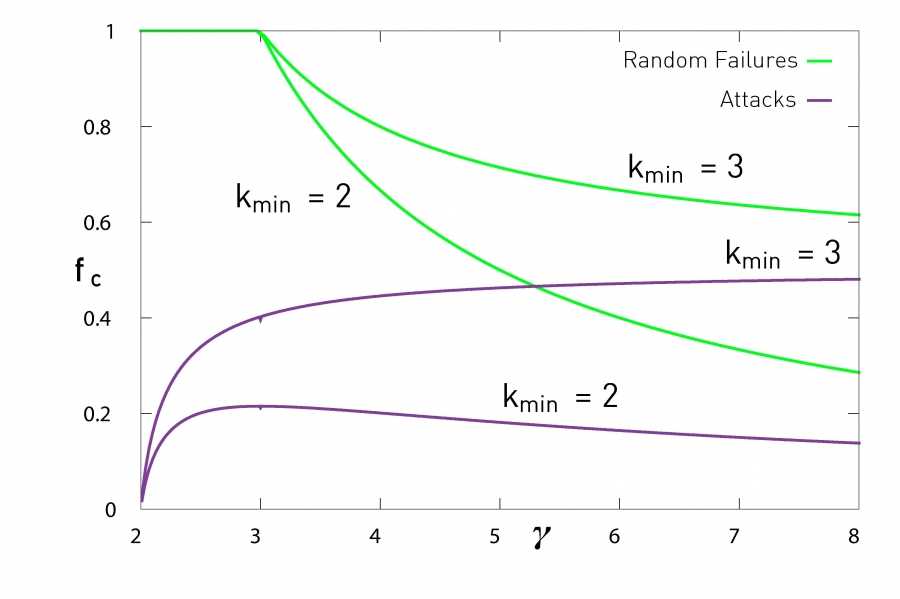
\[f_c = \begin{cases} 1 - \dfrac{1}{\frac{\gamma-2}{3-\gamma} k_{\text{min}} ^{\gamma-2} k_{\text{max}}^{3-\gamma} -1} & \text{if } 2 < \gamma < 3 \\ 1 - \dfrac{1}{\frac{\gamma-2}{\gamma-3} k_{\text{min}} - 1} & \text{if } \gamma > 3 \\ \end{cases}\] $ where \(k_{\text{min}}\) and \(k_{\text{max}}\) are the minimum and maximum degree. (Visualization)

Key Insight: Scale-free networks are remarkably robust to random failures.

🤔 Questions

• ❓ Question #1: If scale-free networks are so robust to random failures, what’s their weakness?
  • Scale-free networks are fragile under targeted attacks.
• ❓ Question #2: What type of attack is the most effective and why?
  • Removing the highest degree node and then the second highest degree node, and so on, is the most effective.
  • …because the critical fraction depends on \(k_{\text{max}}\).

Critical point \(f_c\) for targeted attacks

A node removal changes the degree distribution from \(P(k)\) to \(P'(k)\). Specifically,

1. A node with degree \(k\) is removed from \(P(k)\), and
2. its neighbors lose 1 degree.

We ask: when does \(P'(k)\) lose the giant component as nodes are removed? This gives:

\[f_c^{\frac{2-\gamma}{1-\gamma}} = \frac{2 + 2^{-\gamma}}{3-\gamma} k_{\min} \left(f_c^{\frac{3-\gamma}{1-\gamma}} - 1\right)\]

• \(f_c\) increases as \(\gamma\) increases, which is in contrast to the random failures case.

• \(f_c\) for the random and targeted attacks converge to the same value as \(\gamma \rightarrow \infty\).

\[f_c^{\frac{2-\gamma}{1-\gamma}} = \frac{2 + 2^{-\gamma}}{3-\gamma} k_{\min} \left(f_c^{\frac{3-\gamma}{1-\gamma}} - 1\right)\]

🤔 Design Challenge

❓ Question: Given what we’ve learned about network vulnerabilities, how would you design a robust network?

Consider: What principles would you use? How would you balance cost, efficiency, and security?

Create a network with Interactive game

Let’s code!

List of all nodes

import igraph
import numpy as np

g = igraph.Graph.Famous("Zachary")
g.vs.indices

Remove a node

node_idx = 0
g.delete_vertices(node_idx)

Component size

components = g.connected_components()
components.sizes() # Sizes of all components
np.max(components.sizes()) # Size of the largest component

Misc:

np.max(a) # Maximum value of a
np.random.choice(a) # Random choice from a
np.argmax(a) # Index of the maximum value of a