Module 04: Friendship paradox
Learning Objectives
- 📚 Understand the friendship paradox
- 🔍 Explore its importance and consequences
- 📊 How to plot degree distribution? (not as easy as it seems!)
- Histogram
- CDF
- CCDF
- Log-log plot
- 🧠 Excess degree distribution
Let’s start with a game!
- 🎮 Play the Vaccination Game
- 💉 Vaccinate strategically to halt virus spread
What is the average number of friends that…
- …you have?
- …your friends have?
Friendship Paradox
Your friends have more friends than you, on average
Friendship Paradox Explained 🤔
- 📊 It’s about measurement, not friendship formation!
- Average # of friends of you = Average over nodes
- Average # of friends of your friends = Average over edges
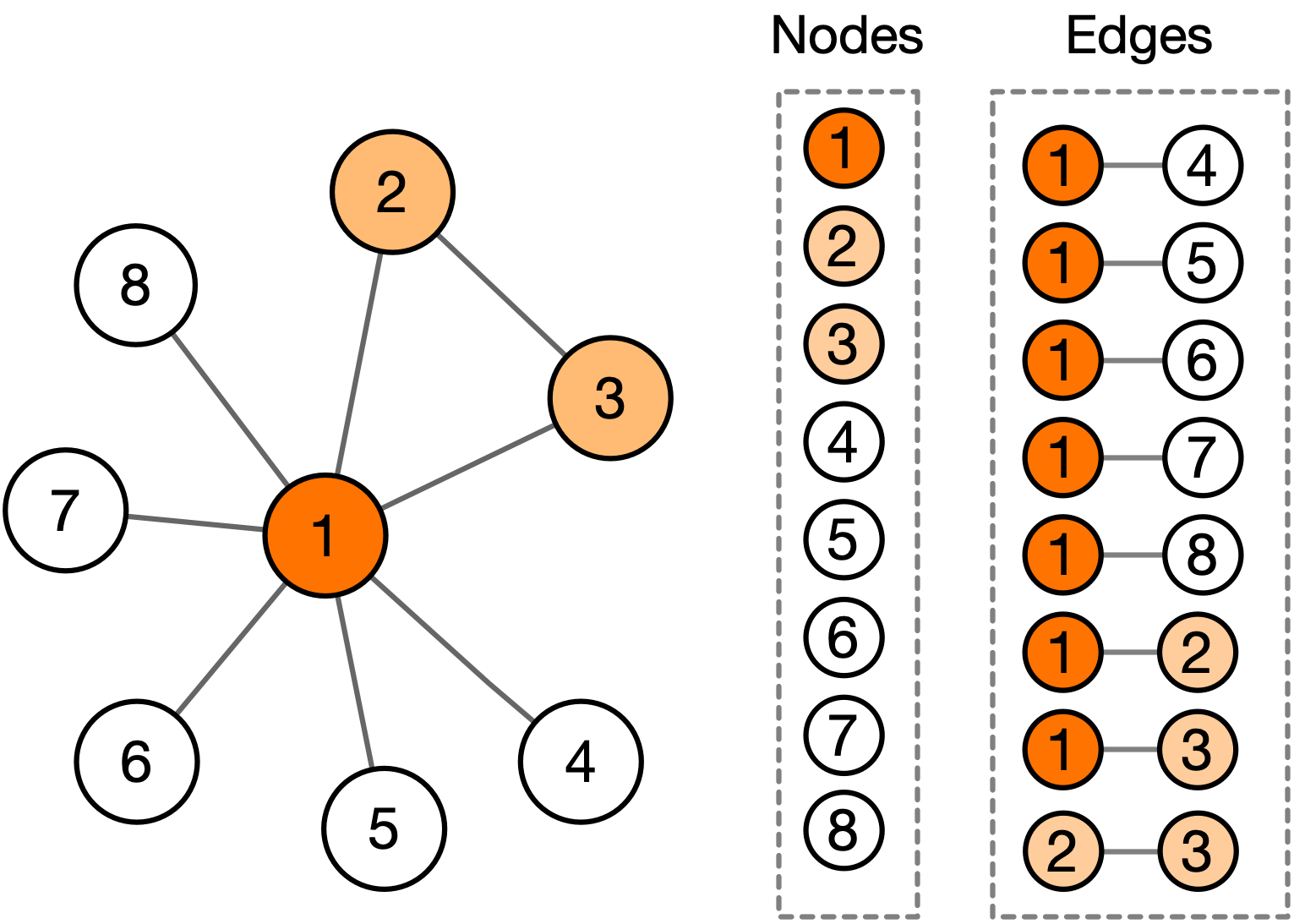
Let’s approach this mathematically.
- Let \(P_0(k)\) be the probability of a node having degree \(k\)
- Let \(P_1(k)\) be the probability of a friend having degree \(k\)
- How does \(P_1(k)\) look like in terms of \(P_0(k)\) and \(k\)?
- Hint:
- Nodes with \(k\) edges appear \(k\) times more likely as a friend of someone than a person with \(1\) edge. Thus, \(P_1(k) \propto \; ????\). To get the actual distribution, you will need \(\langle k \rangle = \sum_{k} k P_0(k)\)
- Compute the average degree of friends over edges
Degree distribution of friends
\(P_1(k) = \frac{k}{\langle k \rangle} P_0(k)\)
Average degree of friends
- \(\langle k_f \rangle = \sum_{k} k P_1(k) = \sum_{k} \frac{k^2}{\langle k \rangle} P_0(k) = \frac{\langle k^2 \rangle}{\langle k \rangle}\)
- 🎮 Play the Vaccination Game
- Think about how the friendship paradox influences your strategy
Degree is crucial for network science!
- Network Robustness
- Epidemic Spreading and Controlling
- Community Detection
- …
Understanding degree distribution is crucial for network analysis. But how do we plot it? 🤔 (it’s not as easy as it seems!)
It’s not as easy as it seems!
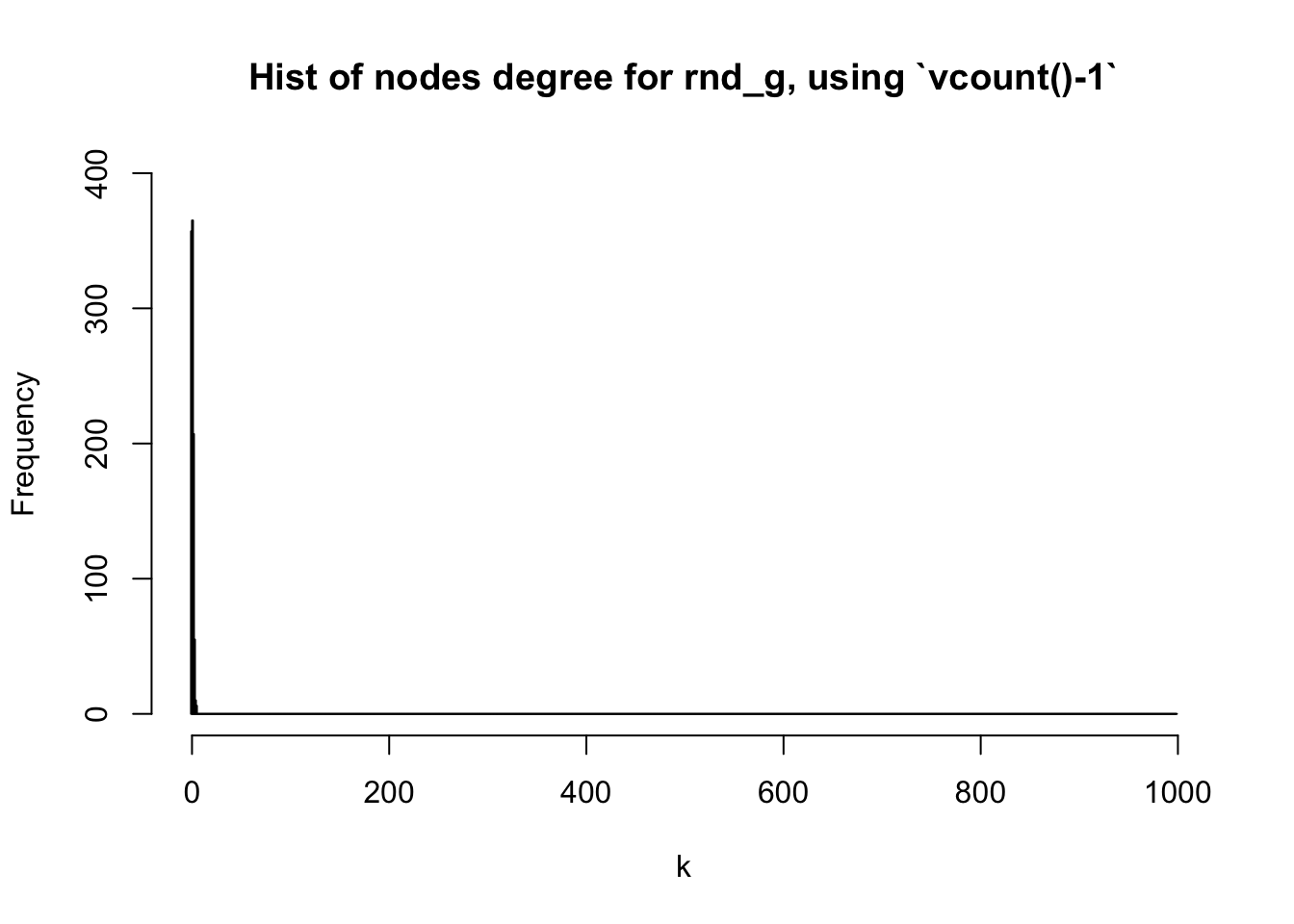
Exercise: Basic visualization techniques
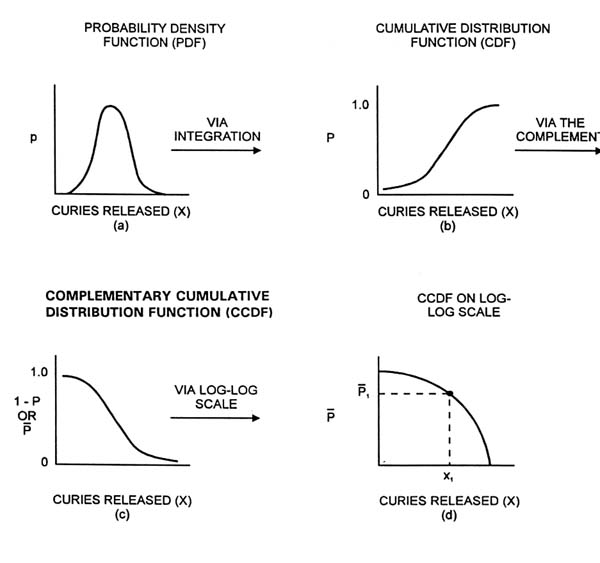
Definitions CDF: \(F(x) = P(X \leq x)\), CCDF: \(\bar{F}(x) = P(X > x) = 1 - F(x)\)