Euler’s solution

Euler consider two cases:

• a node has an even number of edges, or

• a node has an odd number of edges.

When a node has an even number \(2k\) of edges, one can enter and leave the node \(k\) times by crossing different edges.

When a node has an odd number \(2k+1\) of edges, one can enter and leave the node \(k\) times by crossing different edges but leave one last edge to cross. The only way to cross this last edge is that one starts or ends at the node.

Based up on the above reasoning, Euler leads to the following necessary (and later shown as sufficient) conditions:

Euler’s path

There exists a walk that crosses all edges exactly once if and only if all nodes have even number of edges, or exactly two nodes have an odd number of edges.

Back to the Konigsberg bridge problem, every node has an odd number of edges, meaning that there is no way to cross all edges exactly once. What a sad story for the citizens of Konigsberg. But the problem was solved during World War II, where Koingberg was bombarded by Soviet Union, losing two of the seven bridges 🫠.

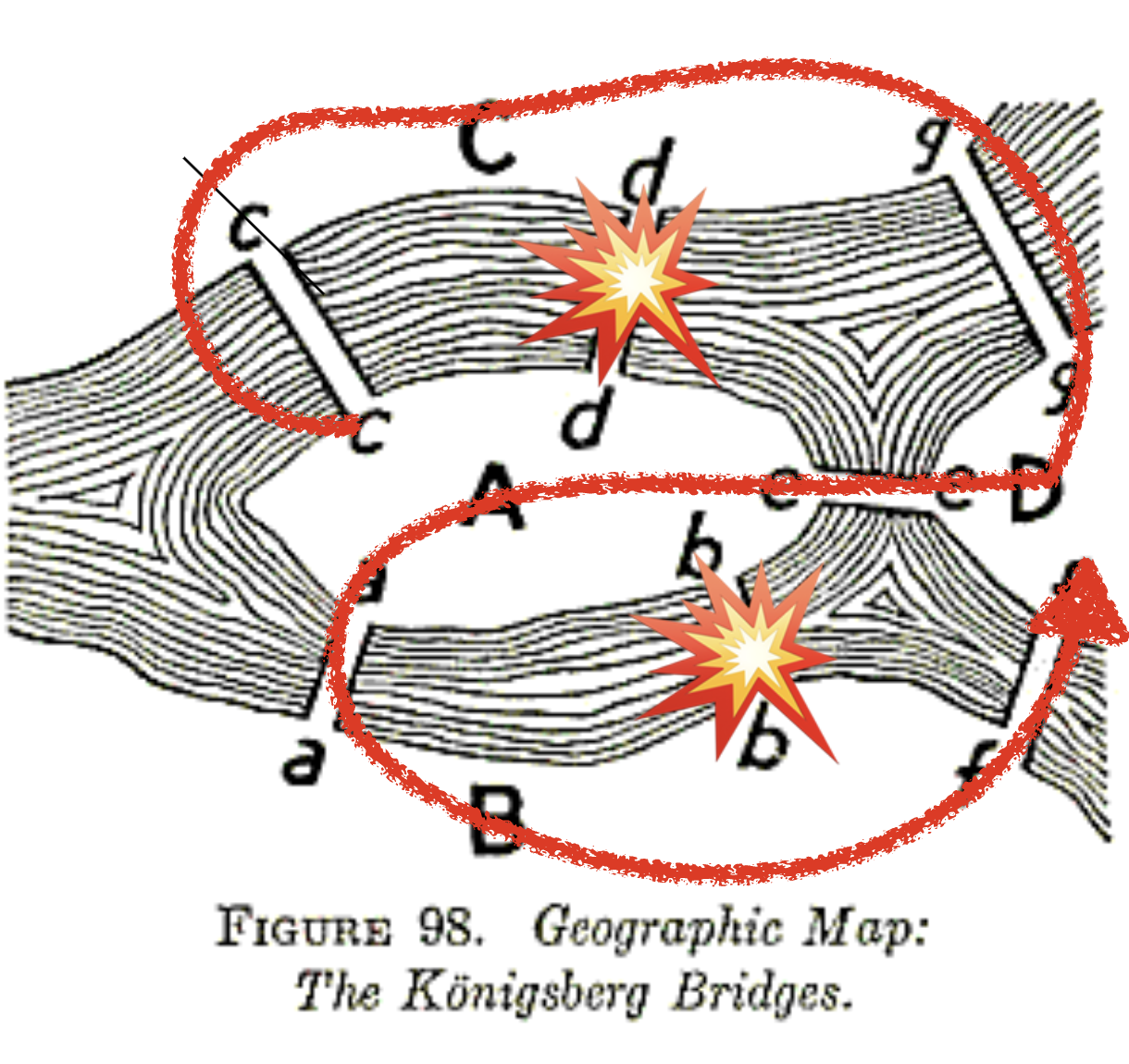
Fig. 3 Two bridges were bombed by Soviet Union, which allows the Euler path to exist.