Advanced Topics in Network Science
1 What is centrality?
Have you ever wondered who the most popular person in your school is? Or which idea is the most important in a subject? Or maybe which movie everyone’s talking about right now? These questions are all about finding out what’s important in a network of people, ideas, or things. In network science, we call this centrality.
Centrality or importance is a question of how important a node is in a network. But the notion of importance is somewhat vague. In what sense we say a node is important? Answering this question needs a specific context, and there are many contexts in which the importance is defined.
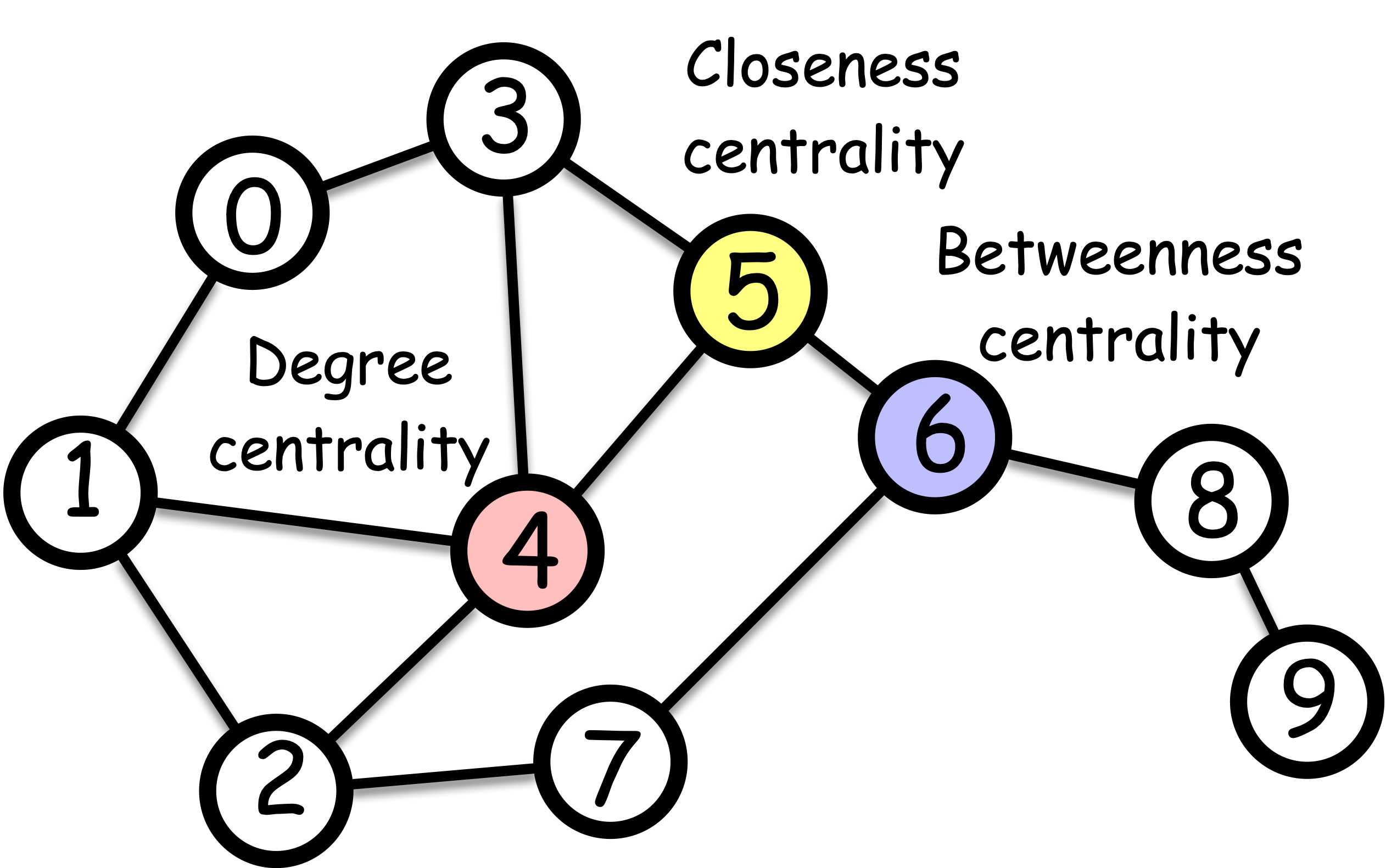
1.1 Different centrality measures
Here we will focus on several popular centrality measures. Let us denote by c_i the centrality of node i throughout this section. Here is a preview of the centrality measures we will cover in this section
| Centrality | Category | Description |
|---|---|---|
| Degree Centrality | Degree | Counts the number of edges connected to a node. |
| Closeness Centrality | Shortest Path | Measures how close a node is to all other nodes in the network. |
| Eccentricity Centrality | Shortest Path | Based on the maximum shortest path distance from a node to any other node. |
| Harmonic Centrality | Shortest Path | Adjusts closeness centrality to work even in disconnected networks. |
| Betweenness Centrality | Shortest Path | Measures the extent to which a node lies on paths between other nodes. |
| Eigenvector Centrality | Walk | Measures a node’s influence based on the influence of its neighbors. |
| HITS (Hub and Authority) Centrality | Walk | Measures the importance of nodes as hubs and authorities in a network. |
| Katz Centrality | Walk | Considers the total number of walks between nodes, with a damping factor. |
| PageRank | Walk | Measures the importance of nodes based on the structure of incoming links. |
Degree centrality
Perhaps the simplest form of cnetrality is degree centrality. It is just the count of the number of edges connected to a node (i.e., the number of neighbors, or degree in network science terminology). The most important node is thus the one with the highest degree.
c_i = d_i = \sum_{j} A_{ij}
where A_{ij} is the adjacency matrix of the network, and d_i is the degree of node i.
Centrality based on shortest path
Let’s talk about an ancient Roman monument called the Milliarium Aureum, also known as the Golden Milestone. It was the starting point for measuring distances on all major roads in the Roman Empire. Emperor Augustus built it when Rome changed from a republic to an empire. The monument not only marked the distances but also represent a centralization of power, where Rome transitioned from a Republic to an Empire. Perhaps the Romans understood the importance of being central in terms of distance, and this concept can be applied to define centrality in networks.
Closeness centrality
Closenes centrality is a measure of how close a node is to all other nodes in the network. A node is central if it is close to all other nodes, which is operationally defined as
c_i = \frac{N - 1}{\sum_{j = 1}^N \text{shortest path length from } j \text{ to } i}
where N is the number of nodes in the network. The numerator, N - 1, is the normalization factor to make the centrality have a maximum value of 1.
Exercise
:class: tip
Create a graph where a node has the maximum closeness centrality of value 1.
Click to see the answer
The simplest example is a star graph, where one node is connected to all other nodes. The node at the center has the highest closeness centrality.
### Harmonic centrality
**Harmonic Centrality** is a measure that adjusts closeness centrality to work even in disconnected networks. The problem with closeness centrality is that it cannot handle disconnected networks. When a network is disconnected, some nodes can't reach others, making their distance infinite. This causes all centrality values to become zero, which isn't very helpful!
To fix this, Beauchamp {footcite:p}`beauchamp1965improved` came up with a clever solution called *harmonic centrality*. It works even when the network is disconnected.
$$
c_i = \sum_{j\neq i} \frac{1}{\text{shortest path length from } j \text{ to } i}
$$
### Eccentricity centrality
**Eccentricity centrality** is baesd on the farthest distance from a node to any other node. The eccentricity centrality is defined as
$$
c_i = \frac{1}{\max_{j} \text{shortest path length from } i \text{ to } j}
$$
These centrality measures provide different perspectives on the importance of nodes based on their accessibility and reachability within the network.
A central node should be close to all other nodes.
Closeness centrality captures the notion of "centrality" in the network. Namely, a node is *central* if it is close to all other nodes.
$$
c_i = \frac{N - 1}{\sum_{j = 1}^N \text{shortest path length from } j \text{ to } i}
$$
where $N$ is the number of nodes in the network. The numerator, $N$, is the normalization factor to make the centrality to have the maximum value of 1.
### Eccentricity centrality
Eccentricity centrality is based on the shortest path distance between nodes, just like the closeness centrality, but it is based on the *maximum* distance as opposed to the average distance like in the closeness centrality.
$$
c_i = \frac{1}{\max_{j} \text{shortest path length from } i \text{ to } j}
$$
### Betweenness centrality
Another notion of centrality is *betweenness centrality*. It considers that a node is important if it lies on many shortest paths between other nodes.
$$
c_i = \sum_{j < k} \frac{\sigma_{jk}(i)}{\sigma_{jk}}
$$
where $\sigma_{jk}$ is the number of shortest paths between nodes $j$ and $k$, and $\sigma_{jk}(i)$ is the number of shortest paths between nodes $j$ and $k$ that pass through node $i$.
:::{#quarto-navigation-envelope .hidden}
[Advanced Topics in Network Science]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyLXRpdGxl"}
[Advanced Topics in Network Science]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXItdGl0bGU="}
[Course Information]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOnF1YXJ0by1zaWRlYmFyLXNlY3Rpb24tMQ=="}
[Welcome]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOi9jb3Vyc2Uvd2VsY29tZS5odG1sV2VsY29tZQ=="}
[About us]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOi9jb3Vyc2UvYWJvdXQuaHRtbEFib3V0LXVz"}
[Discord]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOi9jb3Vyc2UvZGlzY29yZC5odG1sRGlzY29yZA=="}
[Using Minidora]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOi9jb3Vyc2UvbWluaWRvcmEtdXNhZ2UuaHRtbFVzaW5nLU1pbmlkb3Jh"}
[Setup]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOi9jb3Vyc2Uvc2V0dXAuaHRtbFNldHVw"}
[How to submit assignment]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOi9jb3Vyc2UvaG93LXRvLXN1Ym1pdC1hc3NpZ25tZW50Lmh0bWxIb3ctdG8tc3VibWl0LWFzc2lnbm1lbnQ="}
[Introduction]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOnF1YXJ0by1zaWRlYmFyLXNlY3Rpb24tMg=="}
[Networks]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOi9pbnRyby93aHktbmV0d29ya3MuaHRtbE5ldHdvcmtz"}
[M01: Euler Path]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOnF1YXJ0by1zaWRlYmFyLXNlY3Rpb24tMw=="}
[A Stroll, Seven Bridges, and a Mathematical Revolution]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOi9tMDEtZXVsZXJfdG91ci8wMS1jb25jZXB0cy5odG1sQS1TdHJvbGwsLVNldmVuLUJyaWRnZXMsLWFuZC1hLU1hdGhlbWF0aWNhbC1SZXZvbHV0aW9u"}
[Coding Networks in Python]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOi9tMDEtZXVsZXJfdG91ci8wMi1jb2RpbmcuaHRtbENvZGluZy1OZXR3b3Jrcy1pbi1QeXRob24="}
[Exercises]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOi9tMDEtZXVsZXJfdG91ci8wMy1leGVyY2lzZXMuaHRtbEV4ZXJjaXNlcw=="}
[Advanced: Sparse Matrices for Large-Scale Networks]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOi9tMDEtZXVsZXJfdG91ci8wNC1hZHZhbmNlZC5odG1sQWR2YW5jZWQ6LVNwYXJzZS1NYXRyaWNlcy1mb3ItTGFyZ2UtU2NhbGUtTmV0d29ya3M="}
[M02: Small World]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOnF1YXJ0by1zaWRlYmFyLXNlY3Rpb24tNA=="}
[Core Concepts]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOi9tMDItc21hbGwtd29ybGQvMDEtY29uY2VwdHMuaHRtbENvcmUtQ29uY2VwdHM="}
[Efficient Network Representation and Computing Paths]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOi9tMDItc21hbGwtd29ybGQvMDItY29kaW5nLmh0bWxFZmZpY2llbnQtTmV0d29yay1SZXByZXNlbnRhdGlvbi1hbmQtQ29tcHV0aW5nLVBhdGhz"}
[Exercises and Assignments]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOi9tMDItc21hbGwtd29ybGQvMDMtZXhlcmNpc2VzLmh0bWxFeGVyY2lzZXMtYW5kLUFzc2lnbm1lbnRz"}
[Appendix - Brief Introduction to igraph]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOi9tMDItc21hbGwtd29ybGQvMDQtYXBwZW5kaXguaHRtbEFwcGVuZGl4LS0tQnJpZWYtSW50cm9kdWN0aW9uLXRvLWlncmFwaA=="}
[M03: Robustness]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOnF1YXJ0by1zaWRlYmFyLXNlY3Rpb24tNQ=="}
[Core Concepts]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOi9tMDMtcm9idXN0bmVzcy8wMS1jb25jZXB0cy5odG1sQ29yZS1Db25jZXB0cw=="}
[Coding - Network Robustness Analysis]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOi9tMDMtcm9idXN0bmVzcy8wMi1jb2RpbmcuaHRtbENvZGluZy0tLU5ldHdvcmstUm9idXN0bmVzcy1BbmFseXNpcw=="}
[Exercises and Assignments]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOi9tMDMtcm9idXN0bmVzcy8wMy1leGVyY2lzZXMuaHRtbEV4ZXJjaXNlcy1hbmQtQXNzaWdubWVudHM="}
[Exercises and Assignments]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOi9tMDMtcm9idXN0bmVzcy8wNC1hcHBlbmRpeC5odG1sRXhlcmNpc2VzLWFuZC1Bc3NpZ25tZW50cw=="}
[M04: Friendship Paradox]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOnF1YXJ0by1zaWRlYmFyLXNlY3Rpb24tNg=="}
[Core Concepts]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOi9tMDQtbm9kZS1kZWdyZWUvMDEtY29uY2VwdHMuaHRtbENvcmUtQ29uY2VwdHM="}
[Visualizing Degree Distributions in Python]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOi9tMDQtbm9kZS1kZWdyZWUvMDItY29kaW5nLmh0bWxWaXN1YWxpemluZy1EZWdyZWUtRGlzdHJpYnV0aW9ucy1pbi1QeXRob24="}
[Exercises]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOi9tMDQtbm9kZS1kZWdyZWUvMDMtZXhlcmNpc2VzLmh0bWxFeGVyY2lzZXM="}
[M05: Clustering]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOnF1YXJ0by1zaWRlYmFyLXNlY3Rpb24tNw=="}
[Core Concepts]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOi9tMDUtY2x1c3RlcmluZy8wMS1jb25jZXB0cy5odG1sQ29yZS1Db25jZXB0cw=="}
[Clustering Algorithms and Implementation]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOi9tMDUtY2x1c3RlcmluZy8wMi1jb2RpbmcuaHRtbENsdXN0ZXJpbmctQWxnb3JpdGhtcy1hbmQtSW1wbGVtZW50YXRpb24="}
[Exercises and Assignments]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOi9tMDUtY2x1c3RlcmluZy8wMy1leGVyY2lzZXMuaHRtbEV4ZXJjaXNlcy1hbmQtQXNzaWdubWVudHM="}
[M06: Centrality]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOnF1YXJ0by1zaWRlYmFyLXNlY3Rpb24tOA=="}
[Advanced Topics in Network Science]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOi9tMDYtY2VudHJhbGl0eS8wMS1jb25jZXB0cy5odG1sQWR2YW5jZWQtVG9waWNzLWluLU5ldHdvcmstU2NpZW5jZQ=="}
[Advanced Topics in Network Science]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOi9tMDYtY2VudHJhbGl0eS8wMi1jb2RpbmcuaHRtbEFkdmFuY2VkLVRvcGljcy1pbi1OZXR3b3JrLVNjaWVuY2U="}
[Advanced Topics in Network Science]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOi9tMDYtY2VudHJhbGl0eS8wMy1leGVyY2lzZXMuaHRtbEFkdmFuY2VkLVRvcGljcy1pbi1OZXR3b3JrLVNjaWVuY2U="}
[M07: Random Walks]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOnF1YXJ0by1zaWRlYmFyLXNlY3Rpb24tOQ=="}
[Advanced Topics in Network Science]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOi9tMDctcmFuZG9tLXdhbGtzLzAxLWNvbmNlcHRzLmh0bWxBZHZhbmNlZC1Ub3BpY3MtaW4tTmV0d29yay1TY2llbmNl"}
[Advanced Topics in Network Science]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOi9tMDctcmFuZG9tLXdhbGtzLzAyLWNvZGluZy5odG1sQWR2YW5jZWQtVG9waWNzLWluLU5ldHdvcmstU2NpZW5jZQ=="}
[Advanced Topics in Network Science]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOi9tMDctcmFuZG9tLXdhbGtzLzAzLWV4ZXJjaXNlcy5odG1sQWR2YW5jZWQtVG9waWNzLWluLU5ldHdvcmstU2NpZW5jZQ=="}
[M08: Embedding]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOnF1YXJ0by1zaWRlYmFyLXNlY3Rpb24tMTA="}
[Advanced Topics in Network Science]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOi9tMDgtZW1iZWRkaW5nLzAxLWNvbmNlcHRzLmh0bWxBZHZhbmNlZC1Ub3BpY3MtaW4tTmV0d29yay1TY2llbmNl"}
[Advanced Topics in Network Science]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOi9tMDgtZW1iZWRkaW5nLzAyLWNvZGluZy5odG1sQWR2YW5jZWQtVG9waWNzLWluLU5ldHdvcmstU2NpZW5jZQ=="}
[Advanced Topics in Network Science]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOi9tMDgtZW1iZWRkaW5nLzAzLWV4ZXJjaXNlcy5odG1sQWR2YW5jZWQtVG9waWNzLWluLU5ldHdvcmstU2NpZW5jZQ=="}
[Advanced Topics in Network Science]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOi9tMDgtZW1iZWRkaW5nLzA0LWFwcGVuZGl4Lmh0bWxBZHZhbmNlZC1Ub3BpY3MtaW4tTmV0d29yay1TY2llbmNl"}
[M09: Graph Neural Networks]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOnF1YXJ0by1zaWRlYmFyLXNlY3Rpb24tMTE="}
[Advanced Topics in Network Science]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOi9tMDktZ3JhcGgtbmV1cmFsLW5ldHdvcmtzLzAxLWNvbmNlcHRzLmh0bWxBZHZhbmNlZC1Ub3BpY3MtaW4tTmV0d29yay1TY2llbmNl"}
[Advanced Topics in Network Science]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOi9tMDktZ3JhcGgtbmV1cmFsLW5ldHdvcmtzLzAyLWNvZGluZy5odG1sQWR2YW5jZWQtVG9waWNzLWluLU5ldHdvcmstU2NpZW5jZQ=="}
[Advanced Topics in Network Science]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOi9tMDktZ3JhcGgtbmV1cmFsLW5ldHdvcmtzLzAzLWV4ZXJjaXNlcy5odG1sQWR2YW5jZWQtVG9waWNzLWluLU5ldHdvcmstU2NpZW5jZQ=="}
[Advanced Topics in Network Science]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1zaWRlYmFyOi9tMDktZ3JhcGgtbmV1cmFsLW5ldHdvcmtzLzA0LWFwcGVuZGl4Lmh0bWxBZHZhbmNlZC1Ub3BpY3MtaW4tTmV0d29yay1TY2llbmNl"}
[Home]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6SG9tZQ=="}
[/index.html]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6L2luZGV4Lmh0bWw="}
[Course]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6Q291cnNl"}
[Welcome]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6V2VsY29tZQ=="}
[/course/welcome.html]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6L2NvdXJzZS93ZWxjb21lLmh0bWw="}
[About]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6QWJvdXQ="}
[/course/about.html]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6L2NvdXJzZS9hYm91dC5odG1s"}
[Discord]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6RGlzY29yZA=="}
[/course/discord.html]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6L2NvdXJzZS9kaXNjb3JkLmh0bWw="}
[Minidora]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6TWluaWRvcmE="}
[/course/minidora-usage.html]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6L2NvdXJzZS9taW5pZG9yYS11c2FnZS5odG1s"}
[Setup]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6U2V0dXA="}
[/course/setup.html]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6L2NvdXJzZS9zZXR1cC5odG1s"}
[Intro]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6SW50cm8="}
[Why Networks?]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6V2h5IE5ldHdvcmtzPw=="}
[/intro/why-networks.html]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6L2ludHJvL3doeS1uZXR3b3Jrcy5odG1s"}
[Foundations]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6Rm91bmRhdGlvbnM="}
[─── M01: Euler Path ───]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI64pSA4pSA4pSAIE0wMTogRXVsZXIgUGF0aCDilIDilIDilIA="}
[Concepts]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6Q29uY2VwdHM="}
[/m01-euler_tour/01-concepts.html]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6L20wMS1ldWxlcl90b3VyLzAxLWNvbmNlcHRzLmh0bWw="}
[Coding]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6Q29kaW5n"}
[/m01-euler_tour/02-coding.html]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6L20wMS1ldWxlcl90b3VyLzAyLWNvZGluZy5odG1s"}
[Exercises]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6RXhlcmNpc2Vz"}
[/m01-euler_tour/03-exercises.html]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6L20wMS1ldWxlcl90b3VyLzAzLWV4ZXJjaXNlcy5odG1s"}
[Advanced]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6QWR2YW5jZWQ="}
[/m01-euler_tour/04-advanced.html]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6L20wMS1ldWxlcl90b3VyLzA0LWFkdmFuY2VkLmh0bWw="}
[─── M02: Small World ───]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI64pSA4pSA4pSAIE0wMjogU21hbGwgV29ybGQg4pSA4pSA4pSA"}
[/m02-small-world/01-concepts.html]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6L20wMi1zbWFsbC13b3JsZC8wMS1jb25jZXB0cy5odG1s"}
[/m02-small-world/02-coding.html]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6L20wMi1zbWFsbC13b3JsZC8wMi1jb2RpbmcuaHRtbA=="}
[/m02-small-world/03-exercises.html]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6L20wMi1zbWFsbC13b3JsZC8wMy1leGVyY2lzZXMuaHRtbA=="}
[Appendix]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6QXBwZW5kaXg="}
[/m02-small-world/04-appendix.html]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6L20wMi1zbWFsbC13b3JsZC8wNC1hcHBlbmRpeC5odG1s"}
[─── M03: Robustness ───]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI64pSA4pSA4pSAIE0wMzogUm9idXN0bmVzcyDilIDilIDilIA="}
[/m03-robustness/01-concepts.html]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6L20wMy1yb2J1c3RuZXNzLzAxLWNvbmNlcHRzLmh0bWw="}
[/m03-robustness/02-coding.html]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6L20wMy1yb2J1c3RuZXNzLzAyLWNvZGluZy5odG1s"}
[/m03-robustness/03-exercises.html]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6L20wMy1yb2J1c3RuZXNzLzAzLWV4ZXJjaXNlcy5odG1s"}
[/m03-robustness/04-appendix.html]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6L20wMy1yb2J1c3RuZXNzLzA0LWFwcGVuZGl4Lmh0bWw="}
[Core Topics]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6Q29yZSBUb3BpY3M="}
[─── M04: Friendship Paradox ───]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI64pSA4pSA4pSAIE0wNDogRnJpZW5kc2hpcCBQYXJhZG94IOKUgOKUgOKUgA=="}
[/m04-node-degree/01-concepts.html]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6L20wNC1ub2RlLWRlZ3JlZS8wMS1jb25jZXB0cy5odG1s"}
[/m04-node-degree/02-coding.html]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6L20wNC1ub2RlLWRlZ3JlZS8wMi1jb2RpbmcuaHRtbA=="}
[/m04-node-degree/03-exercises.html]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6L20wNC1ub2RlLWRlZ3JlZS8wMy1leGVyY2lzZXMuaHRtbA=="}
[─── M05: Clustering ───]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI64pSA4pSA4pSAIE0wNTogQ2x1c3RlcmluZyDilIDilIDilIA="}
[/m05-clustering/01-concepts.html]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6L20wNS1jbHVzdGVyaW5nLzAxLWNvbmNlcHRzLmh0bWw="}
[/m05-clustering/02-coding.html]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6L20wNS1jbHVzdGVyaW5nLzAyLWNvZGluZy5odG1s"}
[/m05-clustering/03-exercises.html]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6L20wNS1jbHVzdGVyaW5nLzAzLWV4ZXJjaXNlcy5odG1s"}
[─── M06: Centrality ───]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI64pSA4pSA4pSAIE0wNjogQ2VudHJhbGl0eSDilIDilIDilIA="}
[/m06-centrality/01-concepts.html]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6L20wNi1jZW50cmFsaXR5LzAxLWNvbmNlcHRzLmh0bWw="}
[/m06-centrality/02-coding.html]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6L20wNi1jZW50cmFsaXR5LzAyLWNvZGluZy5odG1s"}
[/m06-centrality/03-exercises.html]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6L20wNi1jZW50cmFsaXR5LzAzLWV4ZXJjaXNlcy5odG1s"}
[Advanced Topics]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6QWR2YW5jZWQgVG9waWNz"}
[─── M07: Random Walks ───]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI64pSA4pSA4pSAIE0wNzogUmFuZG9tIFdhbGtzIOKUgOKUgOKUgA=="}
[/m07-random-walks/01-concepts.html]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6L20wNy1yYW5kb20td2Fsa3MvMDEtY29uY2VwdHMuaHRtbA=="}
[/m07-random-walks/02-coding.html]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6L20wNy1yYW5kb20td2Fsa3MvMDItY29kaW5nLmh0bWw="}
[/m07-random-walks/03-exercises.html]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6L20wNy1yYW5kb20td2Fsa3MvMDMtZXhlcmNpc2VzLmh0bWw="}
[─── M08: Embedding ───]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI64pSA4pSA4pSAIE0wODogRW1iZWRkaW5nIOKUgOKUgOKUgA=="}
[/m08-embedding/01-concepts.html]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6L20wOC1lbWJlZGRpbmcvMDEtY29uY2VwdHMuaHRtbA=="}
[/m08-embedding/02-coding.html]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6L20wOC1lbWJlZGRpbmcvMDItY29kaW5nLmh0bWw="}
[/m08-embedding/03-exercises.html]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6L20wOC1lbWJlZGRpbmcvMDMtZXhlcmNpc2VzLmh0bWw="}
[/m08-embedding/04-appendix.html]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6L20wOC1lbWJlZGRpbmcvMDQtYXBwZW5kaXguaHRtbA=="}
[─── M09: Graph Neural Networks ───]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI64pSA4pSA4pSAIE0wOTogR3JhcGggTmV1cmFsIE5ldHdvcmtzIOKUgOKUgOKUgA=="}
[/m09-graph-neural-networks/01-concepts.html]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6L20wOS1ncmFwaC1uZXVyYWwtbmV0d29ya3MvMDEtY29uY2VwdHMuaHRtbA=="}
[/m09-graph-neural-networks/02-coding.html]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6L20wOS1ncmFwaC1uZXVyYWwtbmV0d29ya3MvMDItY29kaW5nLmh0bWw="}
[/m09-graph-neural-networks/03-exercises.html]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6L20wOS1ncmFwaC1uZXVyYWwtbmV0d29ya3MvMDMtZXhlcmNpc2VzLmh0bWw="}
[/m09-graph-neural-networks/04-appendix.html]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLWludC1uYXZiYXI6L20wOS1ncmFwaC1uZXVyYWwtbmV0d29ya3MvMDQtYXBwZW5kaXguaHRtbA=="}
:::{.hidden .quarto-markdown-envelope-contents render-id="Zm9vdGVyLWxlZnQ="}
Copyright 2024, Sadamori Kojaku
:::
:::
:::{#quarto-meta-markdown .hidden}
[Advanced Topics in Network Science]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLW1ldGF0aXRsZQ=="}
[Advanced Topics in Network Science]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLXR3aXR0ZXJjYXJkdGl0bGU="}
[Advanced Topics in Network Science]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLW9nY2FyZHRpdGxl"}
[Advanced Topics in Network Science]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLW1ldGFzaXRlbmFtZQ=="}
[]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLXR3aXR0ZXJjYXJkZGVzYw=="}
[]{.hidden .quarto-markdown-envelope-contents render-id="cXVhcnRvLW9nY2FyZGRkZXNj"}
:::
<!-- -->
::: {.quarto-embedded-source-code}
```````````````````{.markdown shortcodes="false"}
# What is centrality?
Have you ever wondered who the most popular person in your school is? Or which idea is the most important in a subject? Or maybe which movie everyone's talking about right now?
These questions are all about finding out what's important in a network of people, ideas, or things. In network science, we call this *centrality.*
Centrality or *importance* is a question of how important a node is in a network.
But the notion of *importance* is somewhat vague.
In what sense we say a node is important?
Answering this question needs a specific *context*, and there are many contexts in which the *importance* is defined.
## Different centrality measures
Here we will focus on several popular centrality measures. Let us denote by $c_i$ the centrality of node $i$ throughout this section.
Here is a preview of the centrality measures we will cover in this section
| Centrality | Category | Description |
|-------------------------|---------------------|-----------------------------------------------------------------------------|
| Degree Centrality | Degree | Counts the number of edges connected to a node. |
| Closeness Centrality | Shortest Path | Measures how close a node is to all other nodes in the network. |
| Eccentricity Centrality | Shortest Path | Based on the maximum shortest path distance from a node to any other node. |
| Harmonic Centrality | Shortest Path | Adjusts closeness centrality to work even in disconnected networks. |
| Betweenness Centrality | Shortest Path | Measures the extent to which a node lies on paths between other nodes. |
| Eigenvector Centrality | Walk | Measures a node's influence based on the influence of its neighbors. |
| HITS (Hub and Authority) Centrality | Walk | Measures the importance of nodes as hubs and authorities in a network. |
| Katz Centrality | Walk | Considers the total number of walks between nodes, with a damping factor. |
| PageRank | Walk | Measures the importance of nodes based on the structure of incoming links. |
### Degree centrality
Perhaps the simplest form of cnetrality is *degree centrality*. It is just the count of the number of edges connected to a node (i.e., the number of neighbors, or *degree* in network science terminology). The most important node is thus the one with the highest degree.
$$
c_i = d_i = \sum_{j} A_{ij}
$$
where $A_{ij}$ is the adjacency matrix of the network, and $d_i$ is the degree of node $i$.
### Centrality based on shortest path
<img src="https://upload.wikimedia.org/wikipedia/commons/thumb/0/0f/Milliarium_Aureum_op_het_Forum_Romanum_te_Rome_Columna_Miliaria_in_Foro_Romano_%28titel_op_object%29_Antieke_monumenten_%28serietitel%29_Antiquae_Urbis_Splendor_%28serietitel%29%2C_RP-P-2016-345-28-1.jpg/1546px-thumbnail.jpg?20191217151048" alt="Roma Foro Romano Miliarium Aureum" width="80%" style="display: block; margin-left: auto; margin-right: auto;">
Let's talk about an ancient Roman monument called the *Milliarium Aureum*, also known as the *Golden Milestone*.
It was the starting point for measuring distances on all major roads in the Roman Empire.
Emperor Augustus built it when Rome changed from a republic to an empire.
The monument not only marked the distances but also represent a centralization of power, where Rome transitioned from a Republic to an Empire.
Perhaps the Romans understood the importance of being central in terms of distance, and this concept can be applied to define *centrality* in networks.
### Closeness centrality
**Closenes centrality** is a measure of how close a node is to all other nodes in the network. A node is central if it is close to all other nodes, which is operationally defined as
$$
c_i = \frac{N - 1}{\sum_{j = 1}^N \text{shortest path length from } j \text{ to } i}
$$
where $N$ is the number of nodes in the network. The numerator, $N - 1$, is the normalization factor to make the centrality have a maximum value of 1.
::: {.callout-note title="Exercise"}
:class: tip
Create a graph where a node has the maximum closeness centrality of value 1.
::: {.callout collapse="true"}
## Click to see the answer
The simplest example is a star graph, where one node is connected to all other nodes. The node at the center has the highest closeness centrality.
<img src="https://upload.wikimedia.org/wikipedia/commons/thumb/4/49/Star_network_7.svg/1920px-Star_network_7.svg.png" alt="Star graph S7" width="50%" style="display: block; margin-left: auto; margin-right: auto;">
Harmonic centrality
Harmonic Centrality is a measure that adjusts closeness centrality to work even in disconnected networks. The problem with closeness centrality is that it cannot handle disconnected networks. When a network is disconnected, some nodes can’t reach others, making their distance infinite. This causes all centrality values to become zero, which isn’t very helpful!
To fix this, Beauchamp {footcite:p}beauchamp1965improved came up with a clever solution called harmonic centrality. It works even when the network is disconnected.
c_i = \sum_{j\neq i} \frac{1}{\text{shortest path length from } j \text{ to } i}
Eccentricity centrality
Eccentricity centrality is baesd on the farthest distance from a node to any other node. The eccentricity centrality is defined as
c_i = \frac{1}{\max_{j} \text{shortest path length from } i \text{ to } j}
These centrality measures provide different perspectives on the importance of nodes based on their accessibility and reachability within the network.
A central node should be close to all other nodes.
Closeness centrality captures the notion of “centrality” in the network. Namely, a node is central if it is close to all other nodes.
c_i = \frac{N - 1}{\sum_{j = 1}^N \text{shortest path length from } j \text{ to } i}
where N is the number of nodes in the network. The numerator, N, is the normalization factor to make the centrality to have the maximum value of 1.
Eccentricity centrality
Eccentricity centrality is based on the shortest path distance between nodes, just like the closeness centrality, but it is based on the maximum distance as opposed to the average distance like in the closeness centrality.
c_i = \frac{1}{\max_{j} \text{shortest path length from } i \text{ to } j}
Betweenness centrality
Another notion of centrality is betweenness centrality. It considers that a node is important if it lies on many shortest paths between other nodes.
c_i = \sum_{j < k} \frac{\sigma_{jk}(i)}{\sigma_{jk}}
where \sigma_{jk} is the number of shortest paths between nodes j and k, and \sigma_{jk}(i) is the number of shortest paths between nodes j and k that pass through node i.
```````````````````