Advanced Topics in Network Science
1 Community detection (pattern matching)
Community detection is an abstract unsupervised problem. It is abstract because there is no clear-cut definition or ground truth to compare against. The concept of a community in a network is subjective and highly context-dependent.
A classical approach to community detection is based on pattern matching. Namely, we first explicitly define a community by a specific connectivity pattern of its members. Then, we search for these communities in the network.
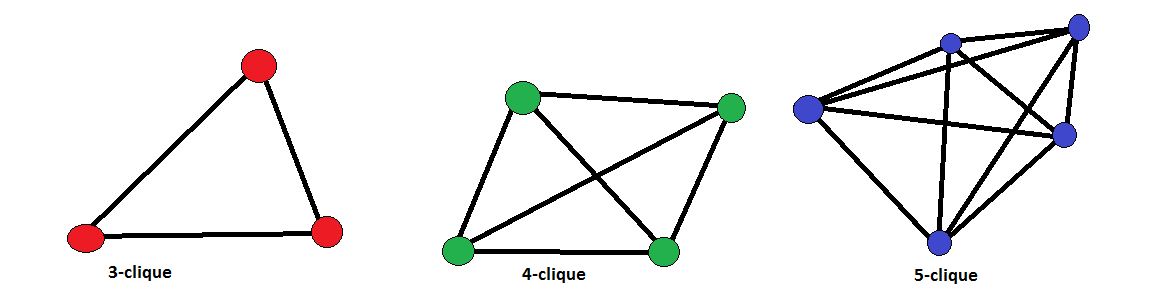
Perhaps, the strictest definition of a community is a clique: a group of nodes all connected to each other. Examples include triangles (3-node cliques) and fully-connected squares (4-node cliques). However, cliques are often too rigid for real-world networks. In social networks, for instance, large groups of friends rarely have every member connected to every other, yet we want to accept such “in-perfect” social circles as communities. This leads to the idea of relaxed versions of cliques, called pseudo-cliques.
Pseudo-cliques are defined by relaxing at least one of the following three dimensions of strictness:
- Degree: Not all nodes need to connect to every other node.
- k-plex: each node connects to all but k others in the group {footcite}
seidman1978graph. - k-core: each node connects to k others in the group {footcite}
seidman1983network.
- k-plex: each node connects to all but k others in the group {footcite}
- Density: The overall connection density can be lower.
- \rho-dense subgraphs, with a minimum edge density of \rho {footcite}
goldberg1984finding.
- \rho-dense subgraphs, with a minimum edge density of \rho {footcite}
- Distance: Nodes can be further apart.
- n-clique, where all nodes are within n steps of each other {footcite}
luce1950connectivity.
- n-clique, where all nodes are within n steps of each other {footcite}
- Combination of the above:
- n-clan and n-club {footcite}
mokken1979cliques - k-truss, a maximal subgraph where all edges participate in at least k-2 triangles {footcite}
saito2008extracting,cohen2009graph,wang2010triangulation. - \rho-dense core, a subgraph with minimum conductance \rho {footcite}
koujaku2016dense.
- n-clan and n-club {footcite}

koujaku2016dense.