Walks, Trails, Paths, and Connectedness

Walks, Trails, Paths

While we have already used the term path, let us make clear its definition, together with other related terms.

• A walk is a sequence of nodes that are connected to form a continous route in a network. For instance, walk (0, 1, 2, 3) is a walk in the graph of the bridges of Konigsberg. But the sequence (0,2,3,1) is not a walk, because the node 0 is not directly connected to node 2.

• A trail is a walk with no repeated edge. For instance, walk (0, 1, 2, 3) is also a trail as it does not cross the same edge twice. But walk (0,2,3,1,3) is not a trail due to the repeated edge (1,3).

• A path is a walk without repeated node. For instance, walk (0,1,2,3) is a path. But walk (0, 1, 2, 1, 2, 3) is not a path due to the repeated node 1 and 2.

• When a walk starts and ends at the same node, it is called a *loop. If the loop is a trail, it is called a circuit. If the loop is a path, it is called a cycle.

Question: Is a path always a trail, and is a trail always a path?

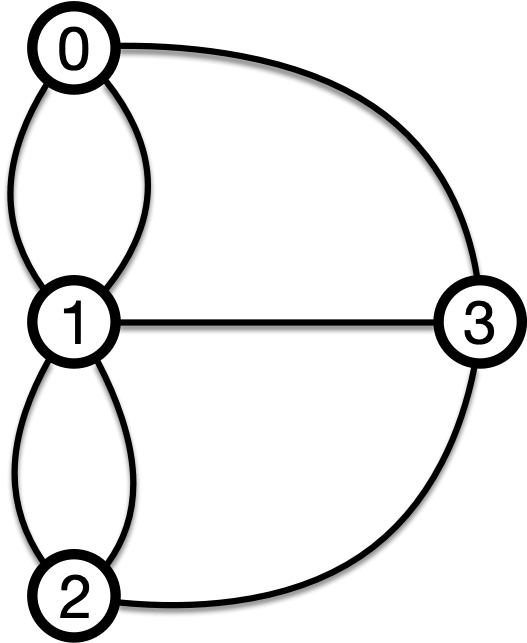
Fig. 6 Labeled Knigsberg graph

• Shortest Path is the path with the smallest number of edges (or nodes) between two nodes. A shortest path from node 0 to 2 is (0, 1, 2). Two nodes can have multiple shortest paths e.g., (0, 3, 2).

• The shortest path length is the number of edges in the shortest path, not the number of nodes! 👈👈

Note

Are there shortest trails and shortest walks? Shortest trails and shortest walks are fundamentally equivalent to shortest paths. A shortest trail must visit each node only once (otherwise it would not be the shortest), and similarly, a shortest walk does not repeat nodes (otherwise it would not be the shortest), both forming a shortest path.

Connectedness

• A network is connected if there is a path between every pair of nodes.

• A network is disconnected if there is no path between some pairs of nodes.

• A connected component of a network is a set of nodes that are connected to each other.

• The giant component of a network is the largest connected component that contains a significant fraction of nodes in the network (in order of the number of nodes).

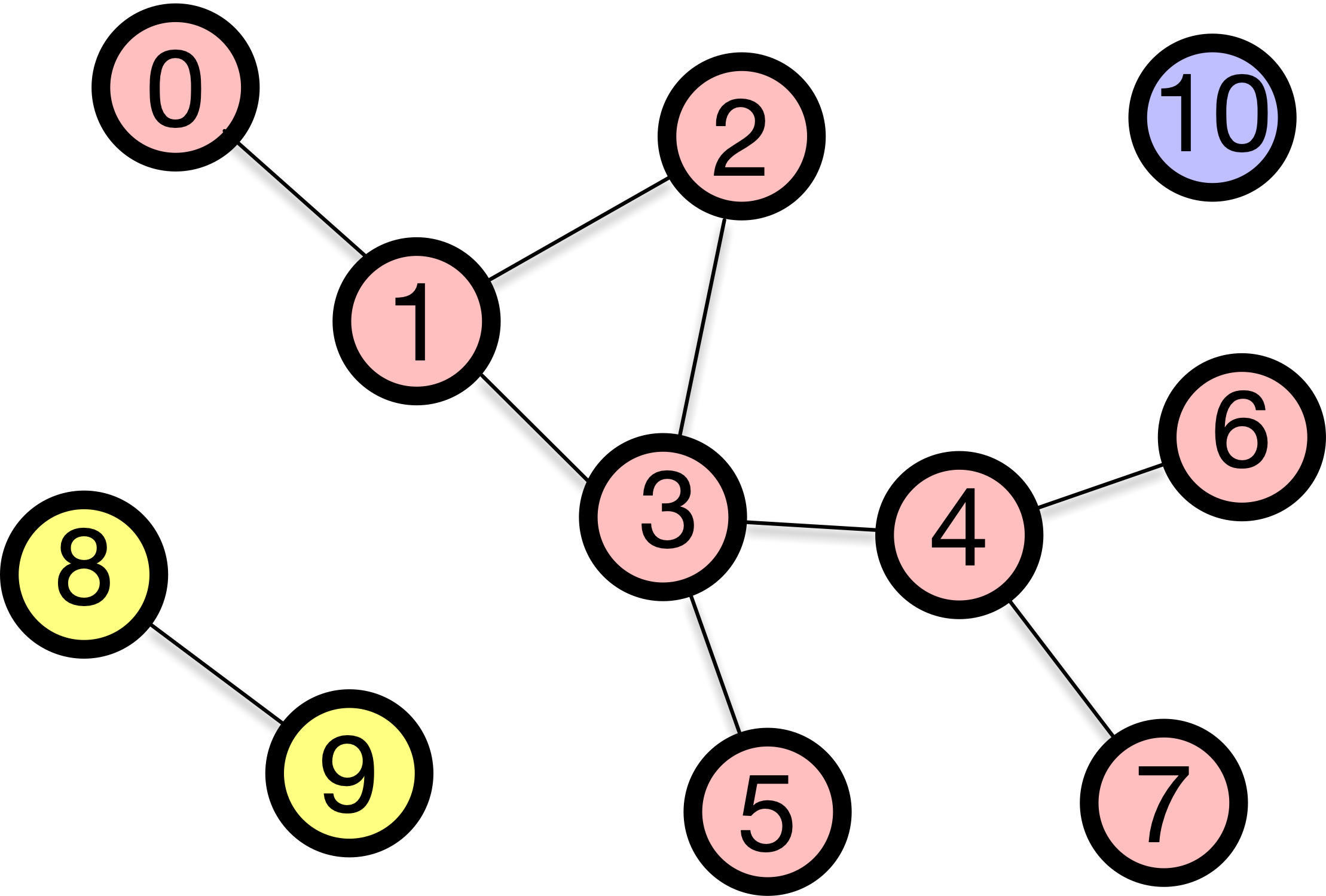
Fig. 7 connected components of a network. the nodes with the same color form a connected component.

Connectedness in directed networks

We call a network is directed if the edges have a direction. Example directed networks include the network of Web pages, the network of friendships on X, the network of citations on academic papers.

In a directed network, a walk must follow the edge directions. Paths, trails, and loops extend similarly to directed networks. But one thing to keep in mind: a walk may not be reversible, meaning there can be a walk from one node to another but not vice versa.

This leads to two different types of connectedness as follows:

• Strong connectedness: A directed network is said to be strongly connected if there is a path from every node to every other node.

• Weak connectedness: A directed network is said to be weakly connected if there is a path from every node to every other node on its undirected counterpart.

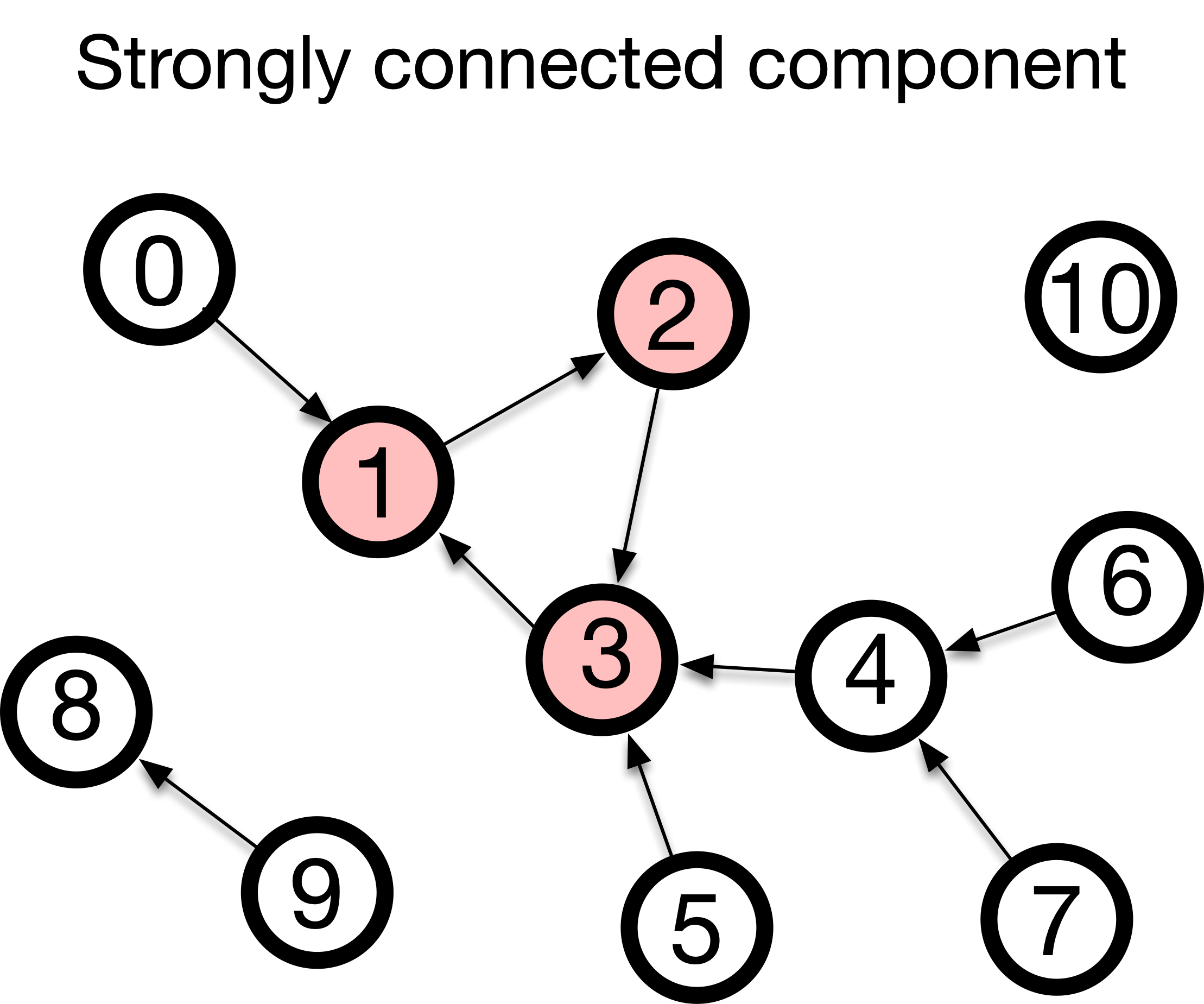
Fig. 8 connected components of a network. the nodes with the same color form a connected component.

Question: Is a strongly-connected component always a weakly-connected component?

In the next section, we will learn how to compute the shortest paths and connected components of a network using a library igraph.