Advanced: Sparse Matrices for Large-Scale Networks

1 The Scale Problem: From Königsberg to Global Networks

Modern networks have billions of nodes—far beyond Königsberg’s 4 landmasses. A dense adjacency matrix for Earth’s 8 billion people would require 512 exabytes of memory!

Real networks are sparse: most node pairs aren’t connected. Edge lists save memory but are inefficient for common operations like finding neighbors or computing degrees.

Think about the following operations:

• Degree: How many friends does a person have?
• Neighbors: Who are the friends of a person?

These operations are very common in network analysis. To do so, you need to go through all the edges in the network. This is not efficient, especially for large networks.

2 Solution: Sparse Matrices

We say a matrix is sparse if the matrix has only a handful of non-zero entries. This is indeed the case for most real-world networks. For such networks, we can use a special type of data type called Compressed Sparse Row (CSR) or Compressed Sparse Column (CSC) to represent the network. This is widely used in many network analysis tools and makes it possible to process large networks in practice.

To learn more, here is a very good blog post by Matt Eding about efficient network representations.

3 SciPy’s Compressed Sparse Row (CSR) Format

Here is a short video explaining the CSR format. Good one to watch if you are visual learner.

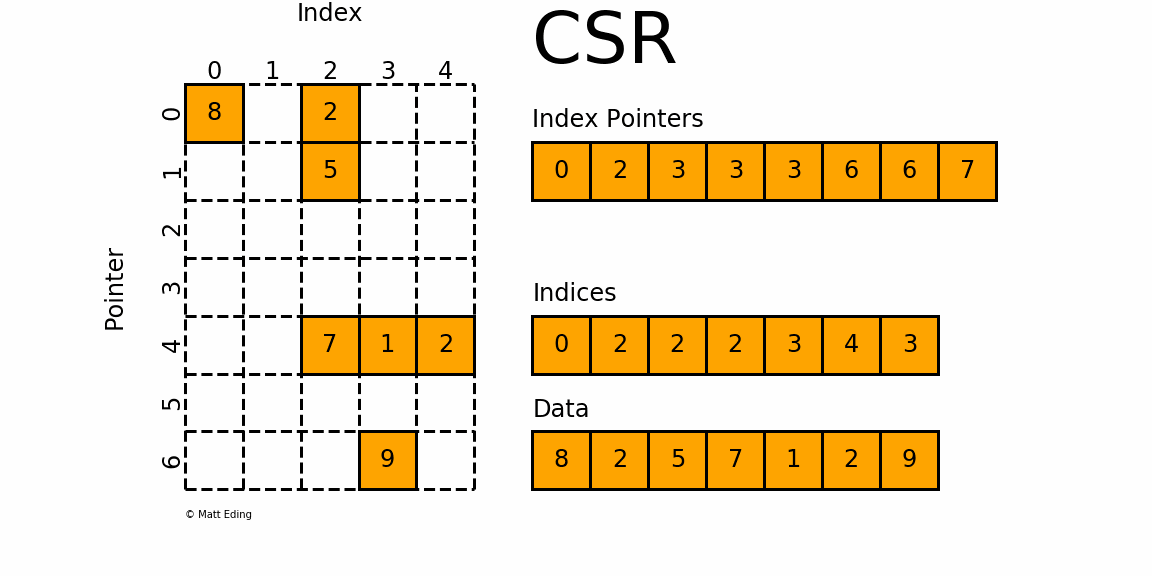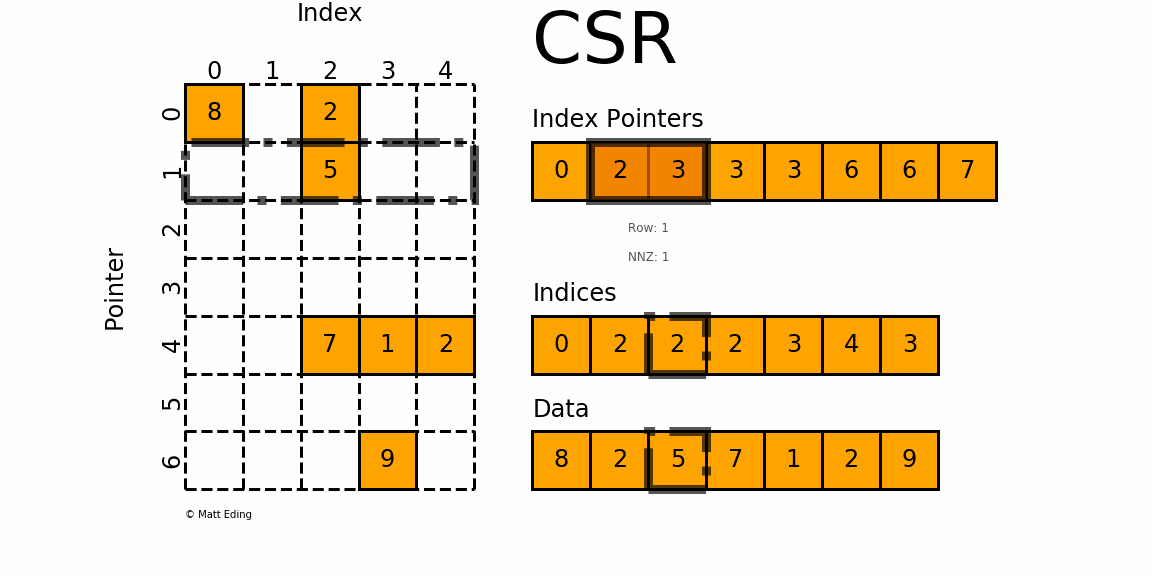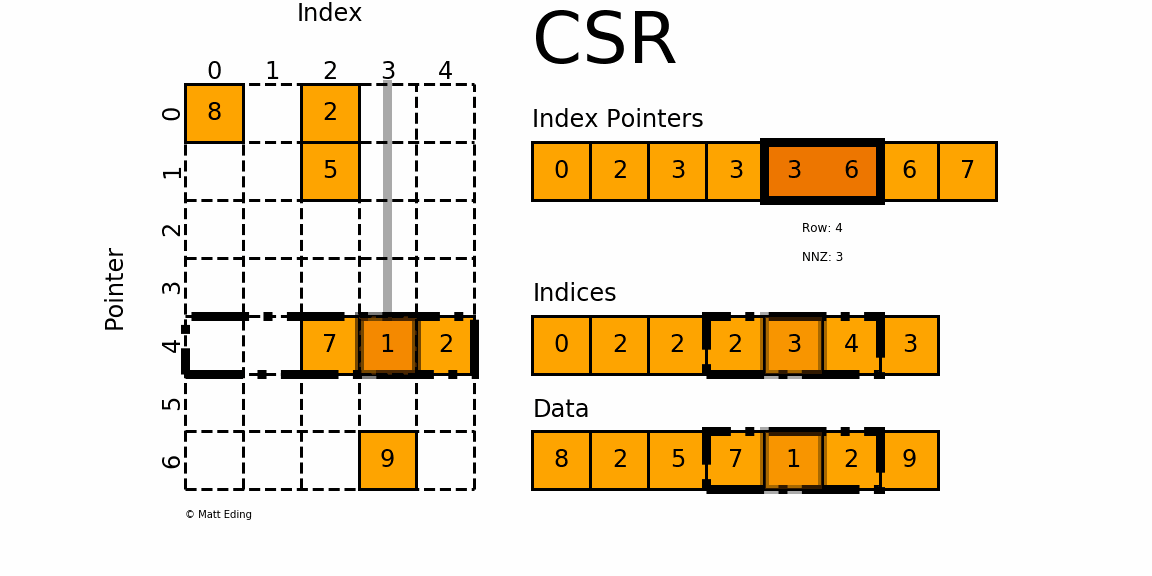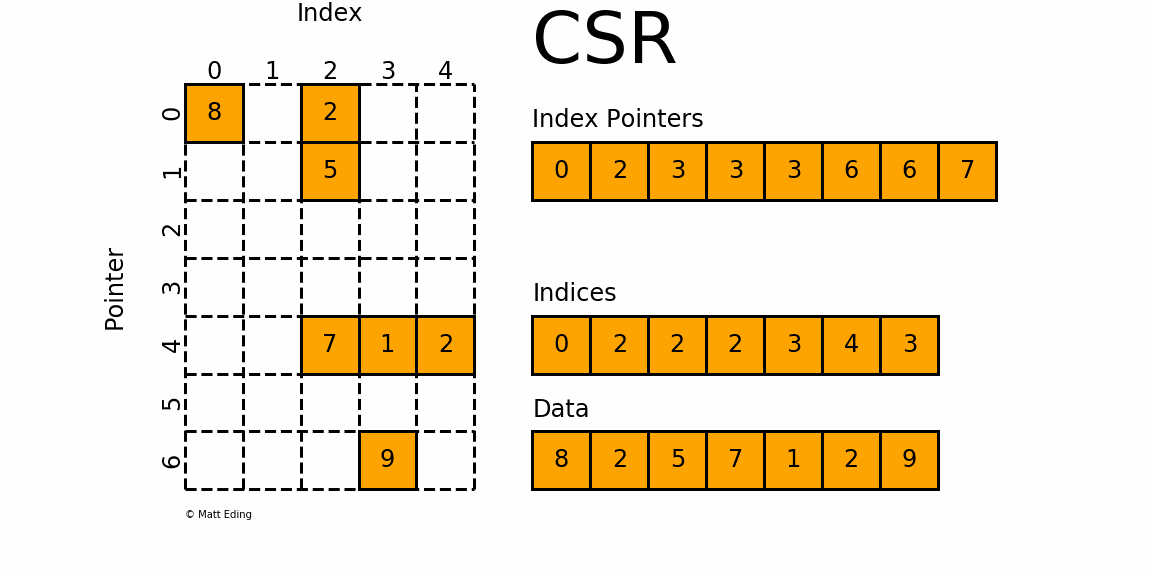Figure 1: A sparse matrix is a matrix with only a handful of non-zero entries represented with a compressed sparse frmat.

CSR stores only non-zero matrix entries using three arrays, making it the standard for large-scale network analysis.

Understanding CSR Structure

CSR format uses three arrays to represent a sparse matrix:

1. data: Contains all non-zero values
2. indices: Column indices of each non-zero value
3. indptr: Row pointers indicating where each row starts in the data array

Memory efficiency: For a sparse matrix with m non-zero entries out of n^2 total entries, CSR uses O(m + n) memory instead of O(n^2). For social networks where m \ll n^2, this is a massive saving!

import numpy as np
from scipy import sparse

# Create a small example network
# Let's represent the same 5-node network from earlier
dense_matrix = np.array([
    [0, 1, 1, 0, 0],  # Node 0 connects to nodes 1, 2
    [1, 0, 1, 1, 0],  # Node 1 connects to nodes 0, 2, 3
    [1, 1, 0, 0, 1],  # Node 2 connects to nodes 0, 1, 4
    [0, 1, 0, 0, 1],  # Node 3 connects to nodes 1, 4
    [0, 0, 1, 1, 0]   # Node 4 connects to nodes 2, 3
])

# Convert to CSR format
csr_matrix = sparse.csr_matrix(dense_matrix)

print("Dense matrix shape:", dense_matrix.shape)
print("CSR matrix shape:", csr_matrix.shape)
print("Non-zero entries:", csr_matrix.nnz)
print("Memory saved: {:.1f}%".format((1 - csr_matrix.nnz / dense_matrix.size) * 100))

Dense matrix shape: (5, 5)
CSR matrix shape: (5, 5)
Non-zero entries: 12
Memory saved: 52.0%

Inside the CSR Format

Let’s examine the internal structure of our CSR matrix:

print("CSR internal arrays:")
print("data (non-zero values):", csr_matrix.data)
print("indices (column positions):", csr_matrix.indices)
print("indptr (row pointers):", csr_matrix.indptr)

# Let's trace through how CSR works
print("\nDecoding CSR structure:")
for i in range(len(csr_matrix.indptr) - 1):
    start = csr_matrix.indptr[i]
    end = csr_matrix.indptr[i + 1]
    row_data = csr_matrix.data[start:end]
    row_indices = csr_matrix.indices[start:end]
    print(f"Row {i}: values {row_data} at columns {row_indices}")

CSR internal arrays:
data (non-zero values): [1 1 1 1 1 1 1 1 1 1 1 1]
indices (column positions): [1 2 0 2 3 0 1 4 1 4 2 3]
indptr (row pointers): [ 0  2  5  8 10 12]

Decoding CSR structure:
Row 0: values [1 1] at columns [1 2]
Row 1: values [1 1 1] at columns [0 2 3]
Row 2: values [1 1 1] at columns [0 1 4]
Row 3: values [1 1] at columns [1 4]
Row 4: values [1 1] at columns [2 3]

How CSR Works

For row i, the non-zero values are stored in data[indptr[i]:indptr[i+1]] with their column positions in indices[indptr[i]:indptr[i+1]].

For example, if indptr[0] = 0 and indptr[1] = 2, then row 0 has non-zero values data[0:2] at columns indices[0:2].

Creating CSR Matrices from Edge Lists

The most common way to create network CSR matrices is from edge lists:

# Define our network as an edge list
edges = [
    (0, 1), (0, 2),  # Node 0 connections
    (1, 2), (1, 3),  # Node 1 connections
    (2, 4),          # Node 2 connections
    (3, 4)           # Node 3 connections
]

# Extract source and target nodes
sources = [edge[0] for edge in edges]
targets = [edge[1] for edge in edges]

# For undirected graphs, add reverse edges
all_sources = sources + targets
all_targets = targets + sources

# Create data array (all ones for unweighted graph)
data_values = np.ones(len(all_sources))

# Create CSR matrix directly from edge list
n_nodes = 5
csr_from_edges = sparse.csr_matrix(
    (data_values, (all_sources, all_targets)),
    shape=(n_nodes, n_nodes)
)

print("CSR from edge list:")
print(csr_from_edges.toarray())

CSR from edge list:
[[0. 1. 1. 0. 0.]
 [1. 0. 1. 1. 0.]
 [1. 1. 0. 0. 1.]
 [0. 1. 0. 0. 1.]
 [0. 0. 1. 1. 0.]]

Efficient Operations with CSR

CSR format enables efficient network operations that would be slow with dense matrices:

# Node degrees - sum each row
degrees = np.array(csr_matrix.sum(axis=1)).flatten()
print("Node degrees:", degrees)

# Find neighbors of node 1
node_1_neighbors = csr_matrix.indices[csr_matrix.indptr[1]:csr_matrix.indptr[2]]
print("Node 1 neighbors:", node_1_neighbors)

# Matrix multiplication for 2-hop paths
two_hop_matrix = csr_matrix @ csr_matrix
print("Two-hop connections (shows paths of length 2):")
print(two_hop_matrix.toarray())

Node degrees: [2 3 3 2 2]
Node 1 neighbors: [0 2 3]
Two-hop connections (shows paths of length 2):
[[2 1 1 1 1]
 [1 3 1 0 2]
 [1 1 3 2 0]
 [1 0 2 2 0]
 [1 2 0 0 2]]

Matrix multiplication: @ is the matrix multiplication operator in SciPy and NumPy. It is equivalent to np.dot.

Memory Comparison: Dense vs CSR

Let’s demonstrate the memory efficiency with a larger, sparser network:

# Create a larger sparse network
n = 1000
density = 0.01  # Only 1% of edges exist

# Generate random sparse matrix
np.random.seed(42)
large_dense = sparse.random(n, n, density=density, format='csr')

print(f"Network size: {n} × {n} = {n**2:,} potential edges")
print(f"Actual edges: {large_dense.nnz:,}")
print(f"Sparsity: {(1 - large_dense.nnz / (n*n)) * 100:.1f}% zeros")
print(f"CSR memory usage: ~{(large_dense.nnz * 2 + n) * 4 / 1024:.1f} KB")
print(f"Dense memory usage: ~{n*n * 4 / 1024:.1f} KB")
print(f"Memory savings: {((n*n * 4) - (large_dense.nnz * 2 + n) * 4) / (n*n * 4) * 100:.1f}%")

Network size: 1000 × 1000 = 1,000,000 potential edges
Actual edges: 10,000
Sparsity: 99.0% zeros
CSR memory usage: ~82.0 KB
Dense memory usage: ~3906.2 KB
Memory savings: 97.9%

CSR for Network Analysis Algorithms

CSR format integrates seamlessly with our previously defined functions:

def is_walk_sparse(sequence, csr_matrix):
    """
    Check if a sequence forms a valid walk using sparse CSR matrix.
    """
    if len(sequence) < 2:
        return True

    sequence = np.array(sequence)
    current_nodes = sequence[:-1]
    next_nodes = sequence[1:]

    # Use CSR matrix indexing - still works with advanced indexing!
    edges_exist = csr_matrix[(current_nodes, next_nodes)]

    # Convert sparse result to array and check
    return np.all(edges_exist == 1)

# Test with our CSR matrix
test_walk = [0, 1, 2, 4, 3, 1]
print(f"Walk {test_walk} is valid: {is_walk_sparse(test_walk, csr_matrix)}")

Walk [0, 1, 2, 4, 3, 1] is valid: True

Best Practices

When to use CSR: - Sparse matrices - Row-based operations (computing degrees, finding neighbors) - Matrix-vector multiplication

When to use dense matrices: - Small networks - Dense networks - Frequent random access to individual entries

There are several different sparse matrix formats such as COO, CSC, and LIL. If you are interested in learning more, you can check out this blog post by Matt Eding. The following video is also a good one to watch.

Advanced CSR Features

# Submatrix extraction - get connections for subset of nodes
subset_nodes = [0, 1, 2]
subgraph = csr_matrix[subset_nodes][:, subset_nodes]
print("Subgraph for nodes [0, 1, 2]:")
print(subgraph.toarray())

# Efficient boolean operations
# Find nodes with degree > 2
high_degree_nodes = np.where(degrees > 2)[0]
print("High degree nodes (> 2 connections):", high_degree_nodes)

# Matrix powers for path counting
paths_3 = csr_matrix ** 3  # Counts 3-step paths
print("3-step path counts:")
print(paths_3.toarray())

Subgraph for nodes [0, 1, 2]:
[[0 1 1]
 [1 0 1]
 [1 1 0]]
High degree nodes (> 2 connections): [1 2]
3-step path counts:
[[2 4 4 2 2]
 [4 2 6 5 1]
 [4 6 2 1 5]
 [2 5 1 0 4]
 [2 1 5 4 0]]

The CSR format transforms network analysis from impossible to practical for large-scale networks. By storing only the essential information (non-zero connections), we can analyze networks with millions of nodes and billions of edges on standard hardware—something that would require exabytes of memory with dense matrices!