import ollama
# Make sure you have Ollama running and a model pulled
# Run: ollama pull mapler/gpt2
MODEL = "mapler/gpt2"
PROMPT = "Hi there! "GPT Inference: Sampling Strategies
This module introduces how GPT generates text through sampling.
You’ll learn:
- What sampling strategies are and how they differ from deterministic selection.
- How to use temperature, top-k, and nucleus sampling to control generation quality.
- The counterintuitive insight that randomness produces better text than always picking the best token.
- Practical consequences for building applications that need coherent, diverse, or creative outputs.
How GPT Generates Text

What do you think happens when GPT generates the next word in a sentence? Here’s the reality: GPT doesn’t output a single word. It outputs a probability distribution over its entire vocabulary (millions of possible tokens, each with a likelihood). The distribution is high-dimensional, making sampling computationally expensive but also rich with alternative paths.
The naive approach is to always pick the highest probability token (greedy sampling), but this creates a deterministic trap where the model falls into repetitive loops. What’s the solution? Controlled randomness. By sampling from the distribution rather than deterministically selecting the peak, we introduce diversity. But blind random sampling produces incoherent text. The challenge is finding the middle ground: sample broadly enough to avoid repetition, but narrowly enough to maintain coherence.
Think of it like improvisational jazz. A musician playing the same note repeatedly (greedy sampling) is boring. Playing random notes (uniform sampling) is noise. The art is in sampling from the most promising notes while occasionally taking creative risks.
Sampling Strategies in Practice
Here is an interactive demo of GPT inference available online at https://static.marimo.app/static/gpt-ar61. You can try different sampling strategies and see the results.
GPT generates text one token at a time, repeatedly sampling from the probability distribution. Let’s examine the strategies for sampling that balance quality and diversity.
First, let’s set up our connection to Ollama:
Greedy Sampling
Greedy sampling always picks the highest probability token. This is deterministic but can lead to repetitive or trapped text. For example, if the model predicts “the” with high probability, it will always predict “the” again. This is the jazz musician stuck on a single note.
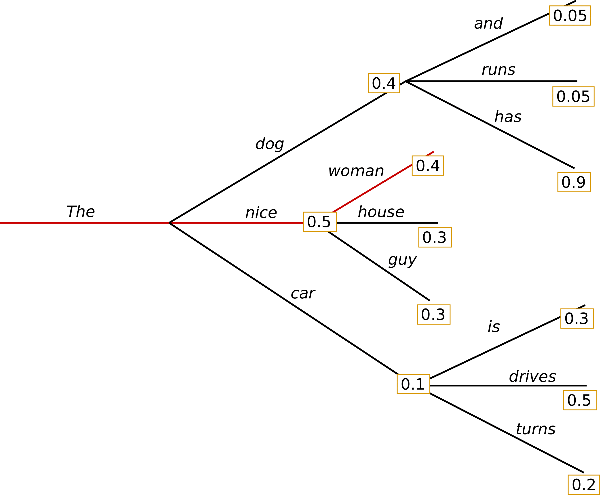
GPT greedy search.
Let’s see greedy sampling in action. We set temperature to 0 to make the sampling deterministic (always picking the highest probability token):
greedy_response = ollama.generate(
model=MODEL,
prompt=PROMPT,
options={
"temperature": 0, # greedy sampling
"num_predict": 20, # max tokens to generate
}
)
print(greedy_response['response']) I'm so glad you're here.
The first thing I did was to make a listThe output is often repetitive because greedy sampling always selects the most probable token at each step. Try running it multiple times. You’ll get the exact same output each time.
Beam Search
What if we could look ahead? Beam search alleviates the repetition problem by taking into account the high-order dependencies between tokens. For example, in generating “The cat ran across the ___“, beam search might preserve a path containing”mat” even if “floor” or “room” have higher individual probabilities at that position. This is because the complete sequence like “mat quickly” could be more probable when considering the token next after “mat”. “The cat ran across the mat quickly” is a more natural phrase than “The cat ran across the floor quickly” when considering the full flow and common linguistic patterns.
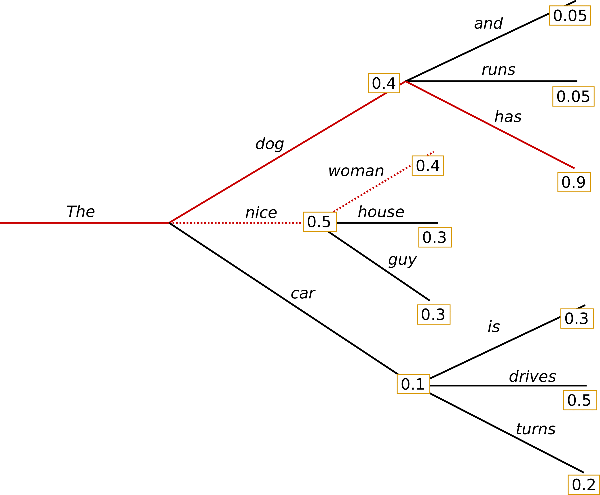
GPT beam search.
How does beam search work? It maintains multiple possible sequences (beams) in parallel, exploring different paths simultaneously. At each step, it expands all current beams, scores the resulting sequences, and keeps only the top-k highest scoring ones. For instance, with a beam width of 3, first beams might be [“The cat ran”, “The cat walked”, “The cat jumped”]. Next step: [“The cat ran across”, “The cat ran through”, “The cat walked across”]. And so on, keeping the 3 most promising complete sequences at each step. This process continues until reaching the end, finally selecting the sequence with highest overall probability. Beam search can be combined with top-k sampling or nucleus sampling. For example, one can sample a token based on top-k sampling or nucleus sampling to form the next beam.
What’s the downside? While beam search often produces high-quality outputs since it considers longer-term coherence, it can still suffer from the problem of repetitive or trapped text. It’s the jazz ensemble playing in perfect harmony, technically excellent but predictable.
Note: Ollama doesn’t natively support beam search through its API. Beam search requires access to the model’s internal scoring mechanism, which is typically implemented at a lower level (using HuggingFace Transformers or direct PyTorch/TensorFlow implementations). For production beam search, you would use libraries like transformers or vLLM.
From Deterministic to Stochastic Sampling
Both greedy and beam search are deterministic. They pick the most likely token at each step, creating a loop where the model always predicts the same tokens repeatedly. What’s the solution? Sample a token from the distribution.
Top-k sampling relaxes the deterministic nature of greedy sampling by selecting randomly from the k most likely next tokens at each generation step. While this introduces some diversity compared to greedy sampling, choosing a fixed k can be problematic. The value of k might be too large for some distribution tails (including many poor options) or too small for others (excluding reasonable options). In our jazz analogy, this is like saying “you can only improvise using these five specific notes”. Sometimes that’s perfect, sometimes it’s too limiting.
top_k_response = ollama.generate(
model=MODEL,
prompt=PROMPT,
options={
"temperature": 1.0, # enable stochastic sampling
"top_k": 10, # restrict to top 10 tokens
"num_predict": 20,
}
)
print(top_k_response['response'])!!!Try running this multiple times. You’ll get different outputs each time because the model samples randomly from the top-k tokens.
What’s a better approach? Nucleus sampling addresses this limitation by dynamically selecting tokens based on cumulative probability. It samples from the smallest set of tokens whose cumulative probability exceeds a threshold p (for example, 0.9). This adapts naturally to different probability distributions: select few tokens when the distribution is concentrated and more when it’s spread out. This approach often provides a good balance between quality and diversity. The jazz musician now has flexibility: when the melody is clear, stick to a few notes. When it’s time to explore, draw from a wider palette.

Nucleus sampling. The image is taken from this blog.
top_p_response = ollama.generate(
model=MODEL,
prompt=PROMPT,
options={
"temperature": 1.0,
"top_p": 0.95, # sample from tokens with cumulative probability >= 0.95
"num_predict": 20,
}
)
print(top_p_response['response']) I'm going to keep getting new ones here when I finally do my bit.
As alwaysNucleus sampling dynamically adjusts the number of candidate tokens based on the probability distribution, making it more adaptive than fixed top-k.
Temperature Control
Temperature (\tau) modifies how “concentrated” the probability distribution is for sampling by scaling the logits before applying softmax:
p_i = \frac{\exp(z_i/\tau)}{\sum_j \exp(z_j/\tau)}
Here z_i are the logits and \tau is the temperature parameter.
What does temperature do to the distribution? Lower temperatures (\tau < 1.0) make the distribution more peaked, making high probability tokens even more likely to be chosen, leading to more focused and conservative outputs. Higher temperatures (\tau > 1.0) flatten the distribution by making the logits more similar, increasing the chances of selecting lower probability tokens and producing more diverse but potentially less coherent text. As \tau \to 0, the distribution approaches a one-hot vector (equivalent to greedy search). As \tau \to \infty, it approaches a uniform distribution. In jazz terms, temperature controls the musician’s mood: low temperature is playing it safe (sticking to the melody), while high temperature is experimental improvisation (sometimes brilliant, sometimes cacophonous).

Temperature controls the concentration of the probability distribution. Lower temperature makes the distribution more peaked, while higher temperature makes the distribution more flat.
Let’s see how temperature affects generation:
for tau in [0.1, 0.5, 1.0, 2.0, 5.0]:
response = ollama.generate(
model=MODEL,
prompt=PROMPT,
options={
"temperature": tau,
"num_predict": 20,
}
)
print(f"τ = {tau}: {response['response']}")τ = 0.1: I'm so happy to be here. I hope you enjoy this post and feel free not only
τ = 0.5: I am sorry for the delay, I hope you enjoyed this post.
The next time around
τ = 1.0: I'm not happy with the idea of having one in my apartment (no, I was thinking
τ = 2.0: ~~~ Please follow me if you would like.
After all of the stuff he wrote that happened
τ = 5.0: !!!
My Santa came up with my own awesome game that you must get and give. WeNotice the pattern: low temperature (τ = 0.1) produces conservative, focused output, medium temperature (τ = 1.0) provides balanced diversity, and high temperature (τ = 5.0) produces creative but potentially incoherent output.
Combining All Strategies
You can combine top-k, top-p, and temperature for fine-grained control:
combined_response = ollama.generate(
model=MODEL,
prompt=PROMPT,
options={
"temperature": 0.7, # moderate randomness
"top_k": 10, # restrict to top 10 tokens
"top_p": 0.95, # within top-k, use nucleus sampling
"num_predict": 20,
}
)
print(combined_response['response']) I hope you enjoy this post and that we'll see more of your stories from our archives.What does this combination do? It restricts candidates to top-k tokens, then applies nucleus sampling, and finally uses temperature to control randomness. This gives you maximum control over the generation process.
The jazz musician now has a framework. Work within these chords (top-k), adapt to the moment (nucleus), and choose your creative intensity (temperature).
Practical Recommendations
What settings should you use? For most applications, use nucleus sampling with p = 0.9 and temperature τ = 0.7. This combination provides a good balance between coherence and creativity. For tasks requiring high factual accuracy (e.g., technical documentation), lower the temperature to τ = 0.3 to make the model more conservative. For creative writing, increase the temperature to τ = 1.0 or higher to encourage exploration. Beam search is useful when you need the single most probable sequence (e.g., machine translation), but it sacrifices diversity. Use it when correctness matters more than variety.
The Key Insight
Generation is sampling. Greedy picks the peak, beam search explores multiple peaks, and stochastic sampling adds controlled randomness. Temperature flattens or sharpens the distribution; nucleus sampling adapts to its shape. The right strategy depends on whether you’re optimizing for accuracy or creativity.